Replications with pentominoes
(a problem suggested by Dario Uri)
It is known that the 12 pentominoes cannot be used to form 4 identical
shapes. (Problem 88 in Golomb's book.)
Dario Uri has proposed (on the newsgroup it.hobby.enigmi)
the following similar problem:
let's take two full sets of pentominoes and let's exchange two
pieces between the sets.
Could now each of the two sets form 4 identical shapes?
Below is one of the possible solutions, obtained exchanging pentominoes N and Y. Livio Zucca and Dario Uri found almost all the solutions.
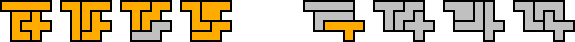
To solve this problem (in the trivial way) I generated all the 3,436,576 15-ominoes, I replicated them 4 times and I searched for tilings. In this way, I obtained 79 half-solutions.
By combining compatible half-solutions I found that 6 exchanges are possible and lead to a total of 10 solutions.

