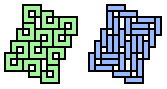
The problem consists in taking two polyominoes, say a tetromino and a pentamino, and finding a figure which can be tessellated indipendently by both the polyominoes. Like these:
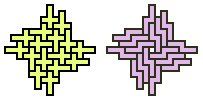
 or
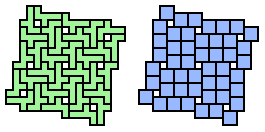
or 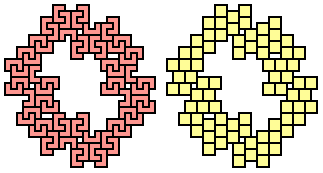
I discovered and became interested in this problem thanks to the great
pages of
Livio Zucca (and in
particular Page1,
Page2, and
Page3)
and of Jorge
Luis Mireles which collect a large number of results, mostly
obtained by hand by a small group of polyomino "heroes".
I can't solve these problems by hand. (I have difficulties even in telling
if two polyominoes are the same apart reflection and rotation...), so
I wrote a little program that searches solutions for me, since I like to
look at them.
In the following pages I collect the results
I obtained running my little program.
I must point out that a large fraction of the solutions I report here has been probably already obtained by other people. I apologize for this, but I'm not really interested in the game of I did it before you did, nor I have the time to compare all the solutions and attribute ownership. I will do it only in the few cases in which the computer program does not find an already known solution.
Visit Col. George Sicherman web site for a large number of beautiful results on this and related problems.
I apologize for the names of the polyominoes.
I did most of the work during the Christmas holidays, when I was out of
Internet, so I did not have a model to conform to. After that, I was too
lazy to change all the names...
A list of the polyominoes I have used is here.
Update Col. George Sicherman has found
a lot (at least 100) of wonderful new solutions. These below are just 4 examples, but to contemplate his most amazing accomplishments please visit
his Addendum page.

| Pairs | Web pages | Solved |
| Pentomino - Tetromino | tetrominoes | 58 / 60 |
| Pentomino - Pentomino | pentominoes | 61 / 66 |
| Hexomino - Tromino | trominoes IL | 70 / 70 |
| Hexomino - Tetromino | tetrominoes | 166 / 175 |
| Hexomino - Pentomino | pentominoes | 389 / 420 |
| Hexomino - Hexomino | hexominoes | 550 / 595 |
| Heptomino - Tromino | trominoes IL | 216 / 216 |
| Heptomino - Tetromino | tetrominoes | 473 / 540 |
| Heptomino - Pentomino |
Pentominoes FILN Pentominoes PTUV Pentominoes WXYZ |
1102 / 1296 |
| Octomino - Tromino | tromino I tromino L |
735 / 738 |
| Octomino - Tetromino |
tetromino I tetromino L tetromino N tetromino Q tetromino T |
308 / 369 369 / 369 361 / 369 144 / 369 361 / 369 |
| Octomino - Pentomino | pentominoes | Enneomino - Tetromino | tetromino I tetromino Q |
| Dekamino - Tetromino | tetromino L |