PolyMultiForms

In how many ways must a man tile the plane
Before you call him a math?

The answer my friend is blowin' in the wind
The answer is blowin' in the wind                   [Bob Dylan]    :o)

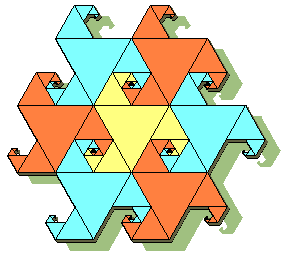
Many Fractals also tile the plane.

This is my contribution to the polyforms.
This page is not a systematic study, but a huddle of ideas, written in the night when I don't sleep. It will be updated frequently. The originality of the ideas is not guaranteed. The unsolved puzzles could be impossible. The work is open to external contributions. Errors are possible. I appreciate the corrections (also of my English :-). A day perhaps I will order it. If you want to read first a systematic treatise about polyforms, see The Poly Pages by Andrew Clarke.
I'm happy when I receive an email.

PolyScalenes

Theorem: ALL the triangles and ALL the quadrilaterals tile the plane. The demonstration (omitted) is easy. Remember: the internal angles sum of a triangle is PI and 2PI for a quadrilateral. With a grid of irregular triangles we could do, for example, the TetraScalenes below:

The gastropod... ops! the TetraScalenes tile the plane.

PentaSlimbes

My first love was the Pentominoes. With a grid of irregular quadrilaterals we could do 63 PentaSlimbes and exactly, using the notation of the Pentominoes: 8F, 2I, 8L, 8P, 8N, 4T, 4U, 4V, 4W, 8Y, 4Z and only one X. They are not flippable, but they can rotate of 180°. 63x5=315=21x15. I'm optimist.

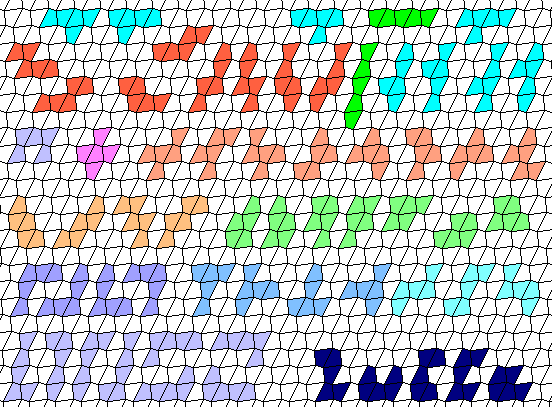
CONTEST

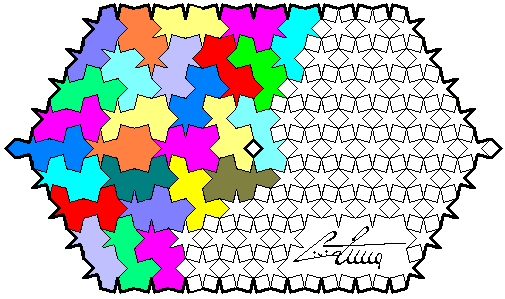
The signature is included in the game. I'll send a free SexeHexeS set to the first who sends me a solution of the puzzle below with the pieces of my "ZuCCa" signature in this exact relative position. Is it egocentrism? No, marketing!

Solution!!!

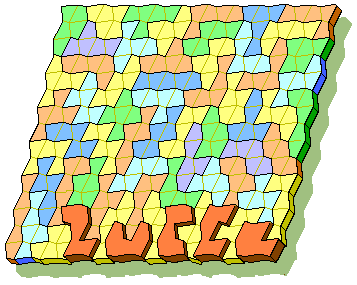
Wed, 14 Jun 2000 14:26:19 -0500
The winner is: Gary Mulkey - Missouri
Bravo!

Here Gary explains to us his approach. Thanks Gary.

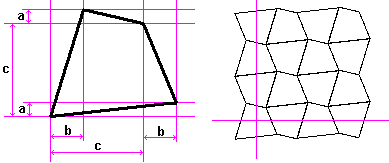
If you use the "Irregular but Not Too Irregular Quadrilateral" below, the grid becomes ortogonal! If you respect the "c" condition also, the grid becomes "squared".

DualBiSlimbes & TriTriTri

Corollaries:

1) The pair of two similar triangles tiles the plane.

2) Each quadrilateral has a partner with complementary angles, together tile the plane.

3) Three similar triangles could tile the plane (with conditions).

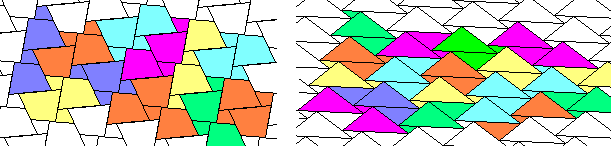
You could do polyforms with grids of many convex or concave irregular polygons. If somebody would try with pentagonal grids, see this page of Ed Pegg Jr. For example, we could compose the puzzle below with one of his pentagonal tiling :

The PentaPenta (sub-set)

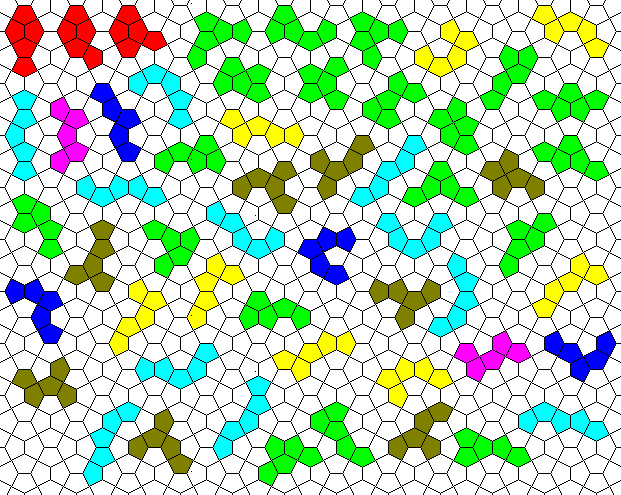
The "Equilateral Cairo" grid, obtained by an equilateral pentagon with two 90° angles, is very interesting and generates non-trivial polyforms:

This is the complete set of 55 (!) PentaCairoes. Brendan Owen sent me the solution and also the images of 17 TetraCairoes, 206 HexaCairos and 718 EptaCairoes [165KB].

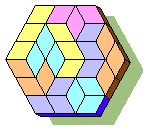
PolyDiamonds

This is one of the last polyforms studied by Miroslav Vicher. The diamond is here formed by two equilateral triangles. Note Miroslav does the pieces on a random grid of diamonds. See on his site other polydiamonds and other polyforms.

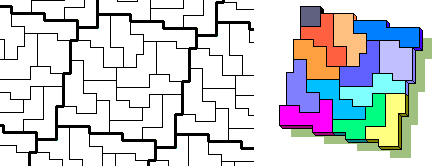
DualBiSquares

Ancient floorings used two squares of different dimensions. I employed this grid to draw the 12 pieces which you see below. They are the possible pieces made with 2 big squares and 2 little squares.

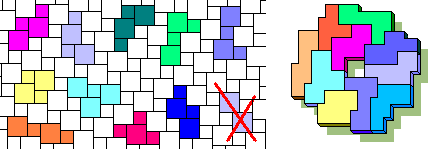
A demonstration of impossibility

It's impossible to tile a compact symmetrical picture. I paint the picture and the pieces with 3 colors. As you see the big squares can only be 9 green + 15 blue or 11+13 or 13+11.

DualBiSquares Puzzle

If I add a big square, I can tile a picture of 5x5 big squares and 24 little squares. Note: I can't put the black square in every position! However the 12 DualBiSquares tile the plane.

Some TriBiSquares

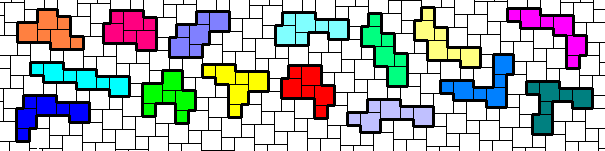
The PolyBiSquares are not flippable.

It's a question of definitions

On a BiSquare grid I have 4 different definitions of polyforms at least, with different results:

1. PolyBiSquares (as you have seen) are the possible pieces made with n big squares and n little squares.

2. PolyPairSquares are the possible pieces made with n pairs of a big square and a little square.

3. PolyDifferentSquares are the possible pieces made with n big or little squares.

4. PolySquares are the possible pieces made with n big or little squares, where the conjunction between two squares must involve an entire edge at least.

Hopefully, I think to find more easily new 'good' sets with the 4th definition. Similar considerations are good for the other PolyBiForms also.

n	n-BiSquares	n-PairSquares	n-DiffSquares	n-Squares
1	1	1	2	2
2	12	11	2	1
3	152	114	8	4
4	2538	1519	...	10
5	...	20769	...	36

20 May 2000 - Brendan Owen sent me his calculation of the BiSquares number. He drew also all the Order 3 [46KB] and Order 4 [236KB] PolyBiSquares.

TetraSquares

They are the possible pieces made with 4 big or little squares on a grid of BiSquares. The conjunction between two squares must involve an entire edge at least (4.th definition). They remember us Tetris, but they are 10, are not flippable, could rotate of 90°.

PentaSquares

They are the possible pieces made with 5 big or little squares on a grid of BiSquares. The conjunction between two squares must involve an entire edge at least (4.th definition). They remember us the Pentominoes, but they are 36 and exactly, using the notation of the Pentominoes: 4F, 2I, 4L, 4P, 4N, 2T, 2U, 2V, 2W, 2X, 4Y, 4Z. They are not flippable, but they could rotate of 90°.

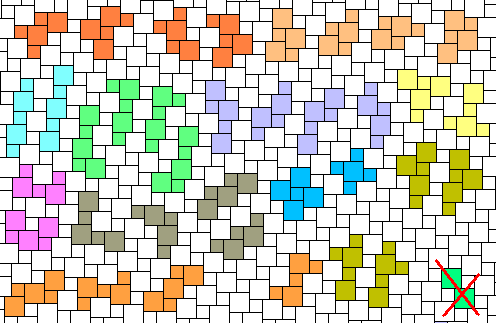
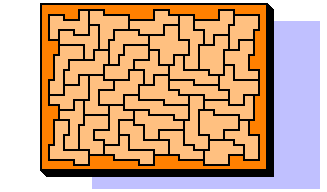
It seems possible to cover symmetrical shapes of 90 big and 90 little squares.

Aug 30th, 2001
The 36 PentaSquares have entered a symmetrical box.
(My solution)

TetraSquareRhombi

They are the possible pieces made with 4 quadrilaterals on a grid of squares and rhombuses (4.th definition). They remember us the Tetrominoes, but they are ten and there are 4 kinds of "L". Below you see a 5x8 solution. The TetraSquareRhombi tile the plane.

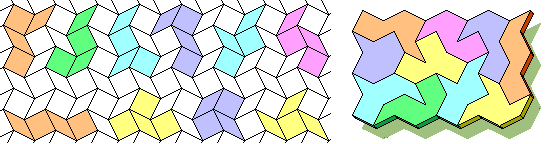
Brendan Owen sends us: "The TetraSquareRhombi problem has 572 solutions and another problem 4x10 has 486". He drew also the pieces up to order 7.

PentaSquareRhombi

They are the possible pieces made with 5 quadrilaterals on a grid of squares and rhombuses (4.th definition). They remember us the Pentominoes, but they are 38 and exactly, using the notation of the Pentominoes: 4F, 2I, 4L, 4P, 4N, 2T, 2U, 3V, 3W, 2X, 4Y, 4Z.

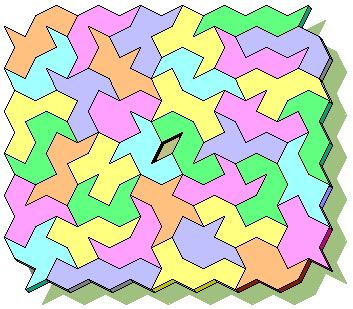
Ohhh! Wonderful!

25 May 2000 - Brendan Owen sent me the first solution. It's agreeable and brilliant. Good job, Brendan!
Note: the PentaSquareRombi don't tile the plane because they are formed by 94 squares and 96 rhombuses. The not-flippable set probably yes.

TetraBricks

I look out of the window (the real window) and I see a wall of bricks. The temptation is too strong. These are the 16 (!) possible flippable TetraBricks. (A TetraBrick is named Brendan because Brendan Owen noted its absence in the first edition of this page).

Brendan Owen sent me the drawing of all Order 5 (n=55) and Order 6 (n=225) PolyBricks. Andrew Clarke informs us that the puzzle could be an old idea, but to build a puzzle in the garden with bricks and cement however amuses myself.

DualOctagonSquares

In my country there are old floors made with octagons and squares. I take 2 octagons and 2 squares to create the pieces below (1.st definition). They are 8 and they can to cover a picture of 4x4 octagons.

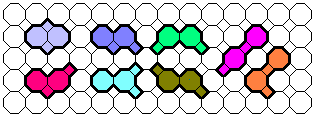
DualOctagonSquares Puzzle

The pieces like "obstinate". I don't find a symmetrical composition or the demonstration that it's impossible. However the pieces tile the plane.

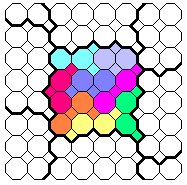
Some TriOctagonSquares

The PolyOctagonSquares are flippable.
Brendan Owen sent me his calculation of the PolyOctagonSquares number:
n    n-OctagonSquares
1    1
2    8
3    80
4    1296
He drew also all the Order 3 [18KB] and Order 4 [114KB] PolyOctagonSquares.

This puzzle is composed in relax with MS Paint and a sub-set of TriOctagonSquares disegned by Brendan. It seems possible to cover rectangular shapes of 240 octagons and 240 squares with alternate squares on the edge. As the Zucca's Puzzle, the superior order sets are reserved to programs and computers of the (imminent?) future.

FourStars&Pentagons

They are the possible ten pieces done with 4 tiles on a grid of regular pentagons and complementary stars (4.th definition). The puzzle is simple but not easy.

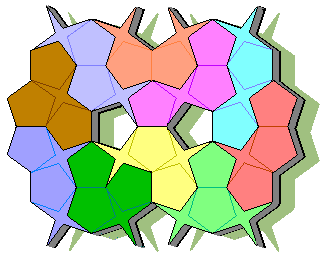
HexagonRhombi

I got the 16 pieces below joining one hexagon and all the combinations of the rhombuses around it, on a grid of hexagons and rhombuses which I saw in the floor of an Italian church of the fourteenth century.

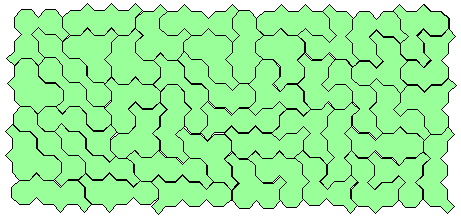
The puzzle is easy. In the 16 pieces and in the grid there are 3 rhombuses for each hexagon on the average. They tile the plane. This set don't respond to any previous definition. You could see here the less lucky DualHexagonHexRhombi (1.st definition) which needs a solution or a demonstration of impossibility.

DualStarHexSquares
(no comment - 1.th definition)

DualStarHexSquares Puzzle

PolyTriForms

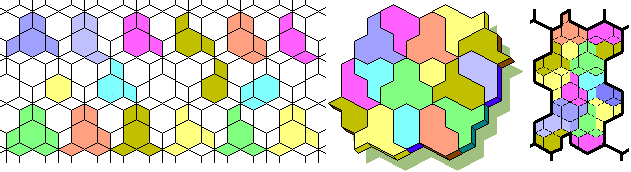
The triangle, the square and the hexagon tile the plane... together also! The ancients already knew it. In the infinite plane there are 2 triangles and 3 squares for each hexagon.

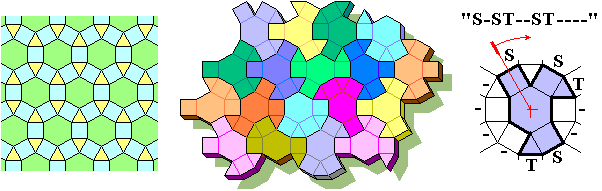
Many definitions of polyforms are possible. For example:

1) All the combinations of 2 triangles and 3 squares around one hexagon. The pieces are 18 and you see up.

2) All the combinations of 1 hexagon, 2 triangles and 3 squares. The pieces are 39. You must add the pieces of this picture.

3) All the combinations of 2 or 3 triangles and 3 or 4 squares around one hexagon for a total of 7 polygons. The pieces are 37 and it seems possible to fill an hexagon of 37 hexagons. Here there is a ascii list of all pieces.

4) All the combinations of possible triangles and squares around the hexagon. The pieces are 214. Here the ascii list.

Each piece of the 1st definition tile the plane:

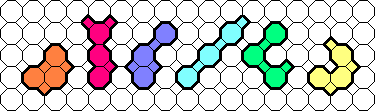
TetraFrogs

Makoto Nakamura drew this frog. I used it to do the polyforms below.
Look at his site.

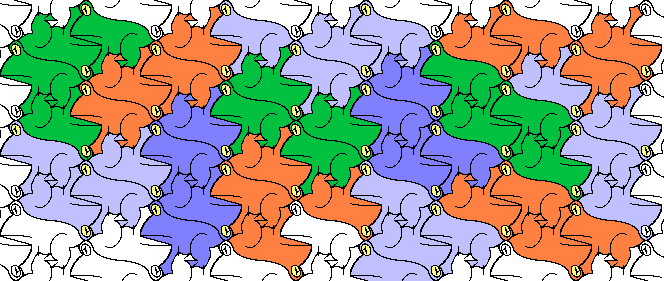
Now we could invent a video game son of the historical Frog and son of the historical Tetris.

The job to do is harder than the done job!

_________________

First edition: May 18th, 2000 - Last revision: Aug 30th, 2001

Goto August 2000 Appendix

| HOME | Pentominoes | More about pentominoes | The cube | 3D pentominoes | Polysexes | Sexominoes | Xominoes | SexeHexeS | SexeHexeS For Sale | More about SexeHexeS | How we did it | Other Sexehex Puzzle | Chronicle | My Solution | Reproduction | Zucca's Puzzle | Domino Puzzle | SexCubes | Dodecaculeus | Tubominoes | Fourier Series of a Square | Order 13 Perfect Square | Fibonacci Machine | Download | Links |