this picture is by my friend Leonardo "Pillow" (see his site)
Click here to see the May 2000 edition.
Click here to see the Aug 2000 edition. (Big Pizza Prize)
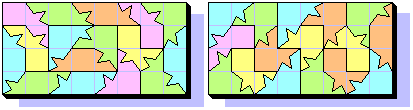
Zucca's Puzzle
Jun 1.st, 2001 - Mark Stubbings solved the Zucca's Puzzle with 1355 pieces and the ragged edge. See here. He found the solution of a 1323 pieces perfect hexagon too. See here.
_________________
Tetrabricks
Since May 2000 nobody sent me solutions with the 16 Tetrabricks. I remember you that, if a polyform series has parity problems, you can use a double set always.
Thousands of solutions.
The PolyBricks are:
Warren Power registered this series on the On-Line Encyclopedia of Integer Sequences with the label A057973. The drawing of the 55 PentaBricks and the 225 HexaBricks are by Brendan Owen. Here you can see a solution with the 55(+1) PentaBricks by Roel Huisman.
_________________
Break & Paste Polyforms
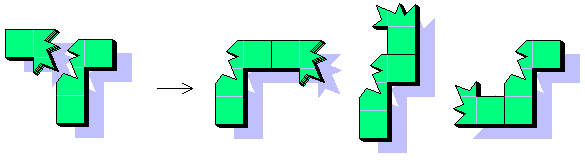
Break a polyform with an irregular fracture. Paste the two pieces along one edge for all the combinations. You'll build Break & Paste Polyforms.
Break & Paste Ominoes (BP1)
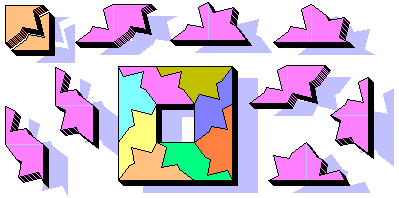
The Break & Paste Ominoes are 8 and can cover a surface of 8 squares. Is it possible to make a 2x4 rectangle? Yes:
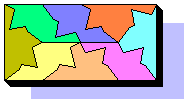
4 solutions only.
Break & Paste Dominoes (BP2a)
See here the generalization.
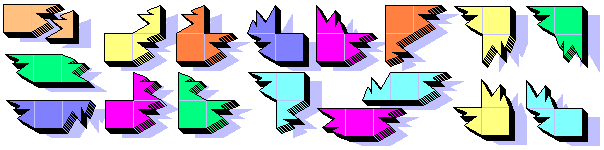
The Break & Paste Dominoes are 16 and can cover a surface of 32 squares. They haven't parity problems.
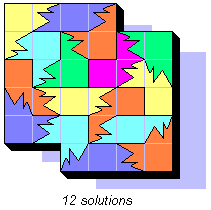
I 
these polyforms! Because they have something of irrational, but they are derived from rules. The puzzles are difficult and the solutions few. I asked the copyrights for this polyforms. If somebody wants to manufacture this game, please contact me here. Whoever wants to build one, he could use this draft.
If you add a tetromino, you could cover a 6x6 square:
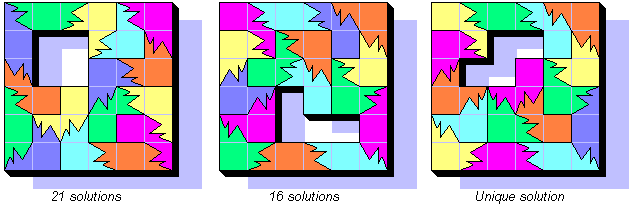
With the "I" tetromino, you could find 53 solutions where the tetromino is always on the corner. With the "T" tetromino, no solutions there are. Do you want to find the math proof?
For the 6x6 square, there are 170 solutions if you add two domino. You could cover a 4x7 rectangle with 14/16 BPD: you'll have 6 solutions only! If you build a 3x11 rectangle with a non-peripheral hole, you have one solution only.
I offer a prize of $1000 to first honest solver of 4x8 rectangle!
There are no parity problems and I don't know math proof of impossibility.
(I think it don't exist :o)
Break & Paste Triominoes (BP3)
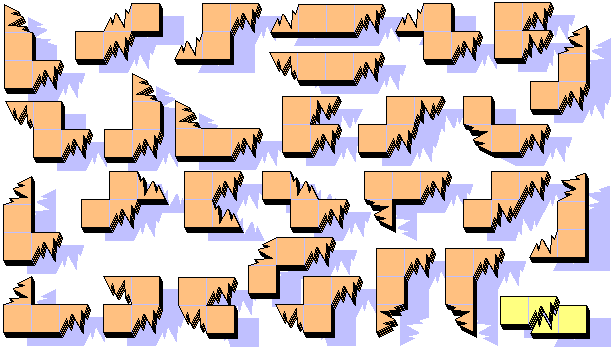
Rules: break a "I" triomino with an irregular fracture along the central diagonal. Paste the two pieces by an edge only, for all the combinations. The BP3 are 28 and can cover a surface of 84 squares, maybe a 7x12 rectangle. They haven't parity problems. The puzzles are very difficult.
A very hard job!
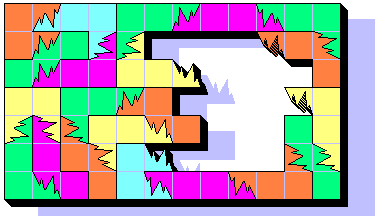
Apr 3th, 2001 - First partial solution of a 12x6 rectangle with 24/28 BP3:
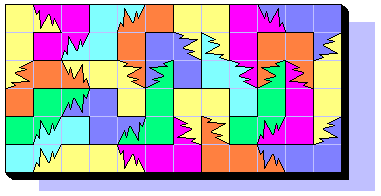
Apr 5th, 2001 - The final solution of a 12x7 rectangle!
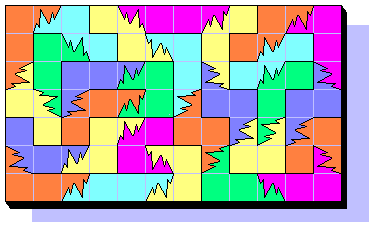
Break & Paste Tetrominoes (BP4)
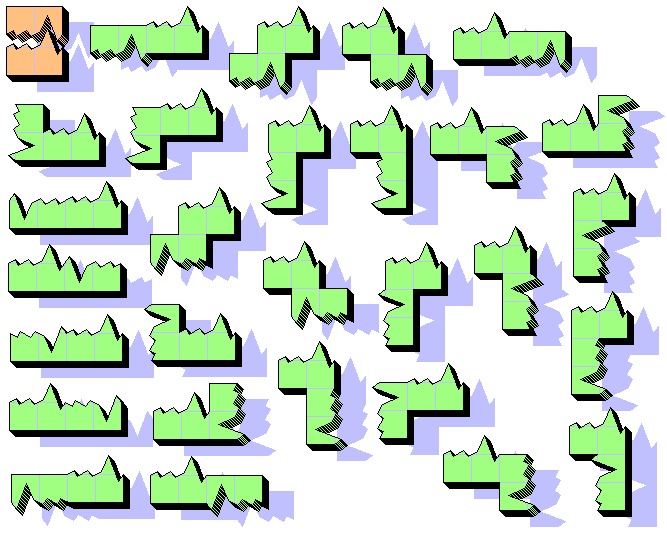
Break a square Tetromino with an irregular fracture along the median line. Paste the two pieces by an unit only, for all the combinations. The BP4 are 28 and can cover a surface of 112 squares, maybe a 8x14 rectangle. The puzzles are few.
12/28 BP4 cover a 6x8 rectangle. Which is biggest possible shape?
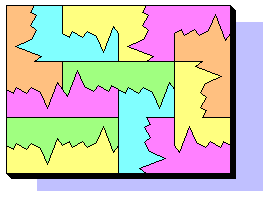
Apr 23th, 2001 - A symmetrical shape with 18/28 BP4:
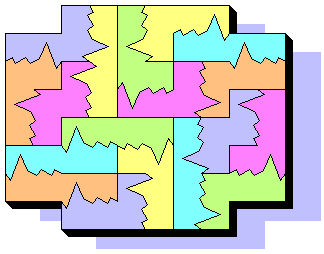
Is it possible to do a symmetrical shape with all the 28 pieces?
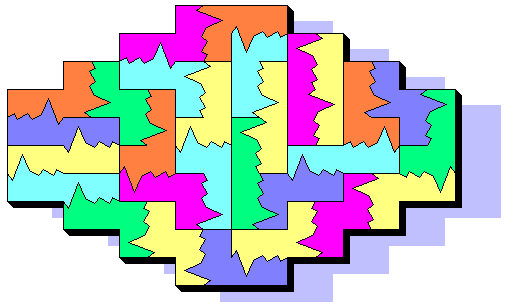
Apr 30th, 2001 - Mario Ricciardi sent the symmetrical shape below with all the 28 Break & Paste Tetrominoes:
Two-Squares-One-Broken (TSOB)
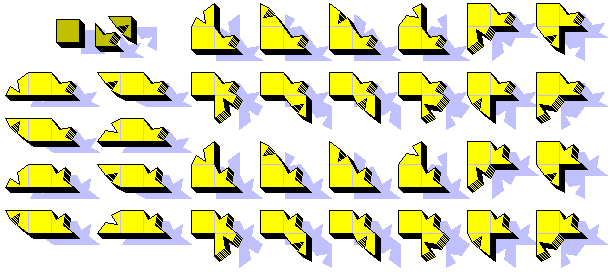
Of two squares, break one with an irregular fracture along the diagonal. Paste the 3 pieces by an edge, for all the combinations. The TSOB are 32 and can cover a surface of 64 squares. I'm ready to bet that the 8x8 shape is possible. I'll publish the first solution I receive.
Aug 6.th, 2001 - Alessandro Fogliati sent me the original handicraft solution below:
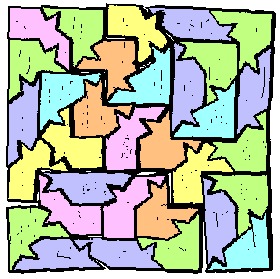
Notice: solution without flipping the pieces.
Aug 12.th, 2001 - Alessandro Fogliati finds a double 4x8 solution:
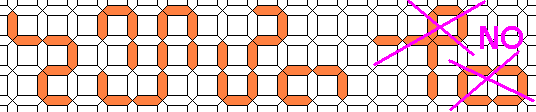
By Gerard's Polyomino Solution Engine he finds more than 600 solutions.
_________________
PolyWorms
Definition: consecutive segments on a triangular, square or hexagonal or complex grid, without loops, intersections or forks. This definition and the calculations below are by Silvio Sergio. Similar polyforms as polyedges, polylines, polysticks or polilati[IT] are by Brian Barwell and Dario Uri.
| Grid\Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Triangular | 1 | 3 | 8 | 32 | 123 | 523 | 2201 | 9443 | 40341 | 172649 | . | . |
| Square | 1 | 2 | 4 | 9 | 22 | 56 | 147 | 388 | 1047 | 2806 | 7600 | 20437 |
| Hexagonal | 1 | 1 | 2 | 3 | 6 | 10 | 19 | 33 | 65 | 118 | 225 | 417 |
PentaWorms
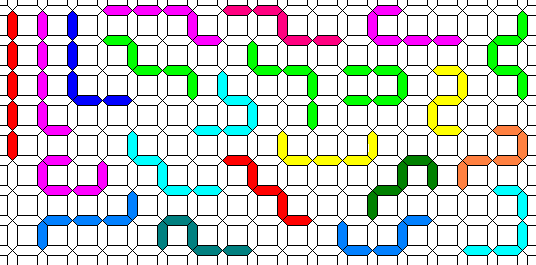
The PentaWorms are 22. They are flippable and you can cross them. It's possible to cover a grate of 6x8 squares: isn't it nice?
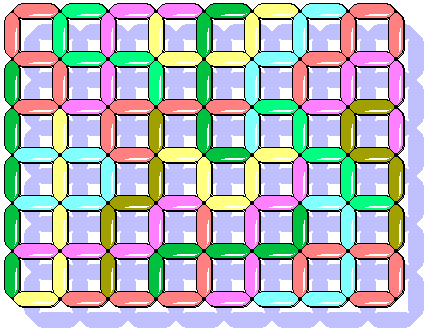
EptaWorms
The EptaWorms are 147. You could see them here. It's probably possible to cover a grate of 14x35 squares.
CONTEST
I offer a free SexeHexeS set
to the first solver who will find before midnight of Christmas 2001 (12/25/2001) the solution of this problem.
TetraSticks
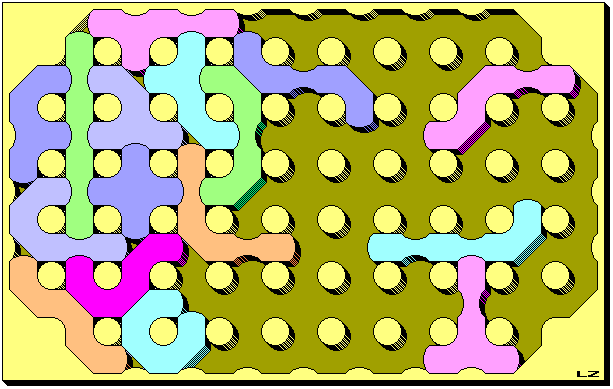
The TetraSticks have parity problems. Two series of TetraSticks can probably fill this symmetrical box. The good work of the friend Wen-Shan Kao inspired me these forms. I'll publish the first solution that I'll receive.
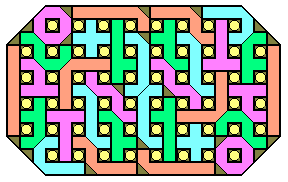
May 4th, 2001
Symmetrical solution by Gerard Putter's Solver and the help of Dario Uri.
_________________
PolyWorms and PolySticks on triangular grid
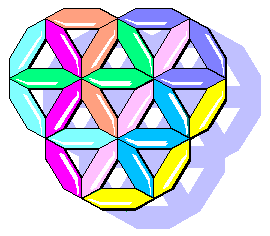
Here up there is a composition of the 8 triangular TriWorms. Below you can see one of 252 solutions by Dario Uri for the triangular TriSticks.
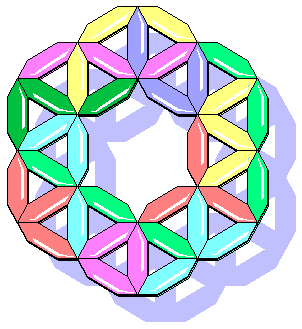
Dario Uri suggest to try PolyWorms on a 3D lattice. It's a good idea, Dario!
_________________
It isn't trivial!
First edition: Mar 29th, 2001 - Last revision: Aug 13th, 2001
|
HOME |
|
e-mail |
Download |
Links |
Chronicle |
|
PENTOMINOES |
|
More about pentominoes |
The cube |
3D pentominoes |
Maximizing |
|
POLYSEXES |
|
Sexominoes |
Xominoes |
Zucca's Puzzle |
Domino Puzzle |
SexCubes |
Dodecaculeus |
Tubominoes |
|
SEXEHEXES |
|
SexeHexeS For Sale |
More about SexeHexeS |
How we did it |
Other Sexehex Puzzle |
My Solution |
Reproduction |
|
POLYMULTIFORMS |
|
Aug 2000 edition |
May 2000 edition |
PolyEdges |
To cover a solid |
Fourier Series of a Square |
Order 13 Perfect Square |
Fibonacci Machine |
Index
