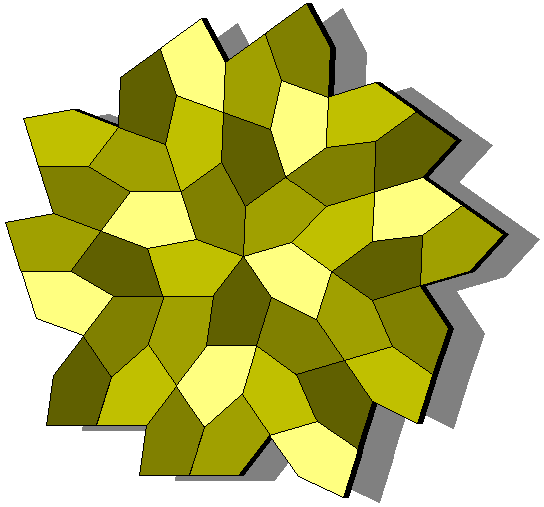
On this page we consider the equilateral pentagon only. If you want to see general pentagon tilings, go on this page, maintained by Ed Pegg Jr.

We want to consider all the equilateral pentagons that, for the particular values of their angles, tile the plane with different topology.

We defined five families of equilateral pentagons that tile the plane:

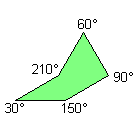
1) With two consecutive angles that their sum is equal to 180°:

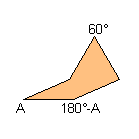
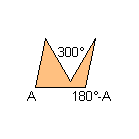
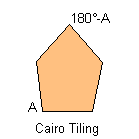
2) With two non-consecutive angles that their sum is equal to 180°:

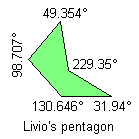
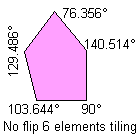
3) With two consecutive angles that their sum is equal to 360°:

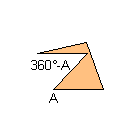
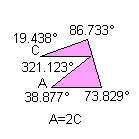
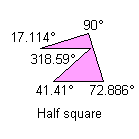
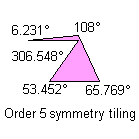
4) With two non-consecutive angles that their sum is equal to 360°:

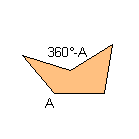
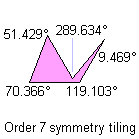
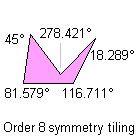
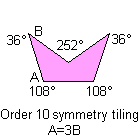
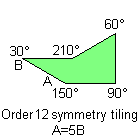
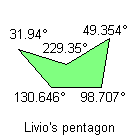
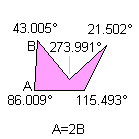
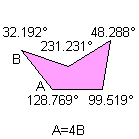
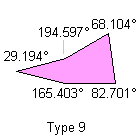
5) Without any of the previous characteristics:

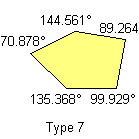
Click each pentagon to see the relative tiling.

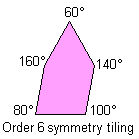
Notice: All the pink or green pentagons tile the plane also as the brown pentagon of their family. A pink or green pentagon tiles the plane with particular topology for the particular value of an other angle. The green pentagons are members of two family and they link an only web-page.