Tetrominoes Challenge
Livio Zucca
This page is currently maintained by Col. George Sicherman.
Please visit his page for updates.
We are searching for the 25 shapes that can be covered by some tetrominoes AND NOT by the others. We'll give precedence to the solutions on the plane with the smallest surface. If you have better solutions, please send me HERE with gif, jpg, bmp, FidoCad or ascii-art format.
| ILNQ | ILNT | ILQT | INQT | LNQT |
 |
 |
 |
 |
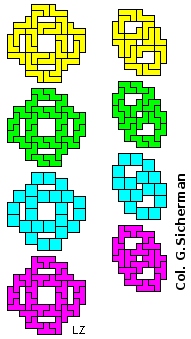 |
| ILN | ILQ | ILT | INQ | INT |
 |
 |
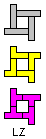 |
 |
 |
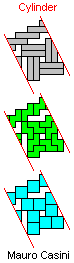
| IQT | LNQ | LNT | LQT | NQT |
 |
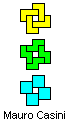 |
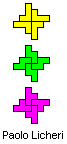 |
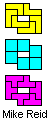 |
 |
| IL | IN | IQ | IT | LN |
 |
 |
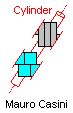 |
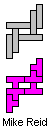 |
 |
| LQ | LT | NQ | NT | QT |
 |
 |
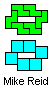 |
 |
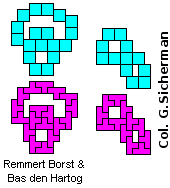 |
Notice:
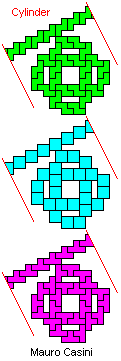
You can see here below, at left, the first IT solution with N= 10. Afterwards, Mike Reid produced two improvements, one with N=8 and the other with N=6. After few hours, I received the solutions of Helmut Postl and Remmert Borst, with N=6 also.

The Mike's solutions are probably direct, on the contrary Helmut and Remmert derived their solutions from others.
For Helmut's solution we can write:
IT = ILT & INT
(I OR T) = (I OR L OR T) AND (I OR N OR T)
for Remmert's solution:
IT = ILQT & INT
(I OR T) = (I OR L OR Q OR T) AND (I OR N OR T)
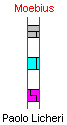
Proof that solutions with an odd number of tetrominoes cannot exist.
The demonstration is of Paolo Licheri.
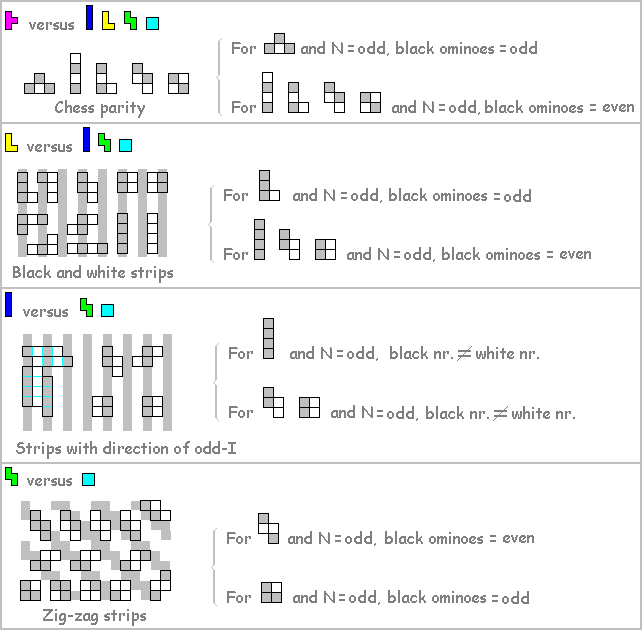
See also:
Pento-tro-dominoes
Pento-tetro-trominoes
LINK:
Visit the wonderful site of Jorge Luis Mireles
_________________
It isn't trivial!
First edition: Dic 24th, 2003 - Last revision: Jan 17th, 2004




 Index
Index




