To cover a solid
In an old problem the pentominoes are folded to cover a cube. Below there are two my solutions. Wen-Shan Kao has many others. The question now is: Are there other regular polyforms sets that cover a regular polyhedron?
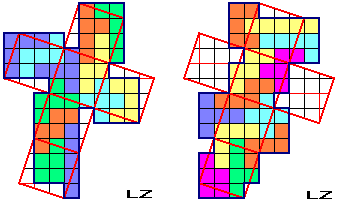
In the pictures and in the table below you could read how many squares a square (or a cube area) contains exactly, and how many triangles are contained in a triangle or on an area of a tetrahedron, an octahedron or an icosahedron.
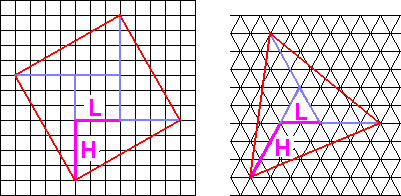
| Nr. | L | H | Square | Cube | Triangle | Tetrahedron | Octahedron | Icosahedron |
| 1 | 0 | 1 | 2 | 12 | 3 | 12 | 24 | 60 |
| 2 | 0 | 2 | 8 | 48 | 12 | 48 | 96 | 240 |
| 3 | 0 | 3 | 18 | 108 | 27 | 108 | 216 | 540 |
| 4 | 0 | 4 | 32 | 192 | 48 | 192 | 384 | 960 |
| 5 | 0 | 5 | 50 | 300 | 75 | 300 | 600 | 1500 |
| 6 | 0 | 6 | 72 | 432 | 108 | 432 | 864 | 2160 |
| 7 | 0 | 7 | 98 | 588 | 147 | 588 | 1176 | 2940 |
| 8 | 0 | 8 | 128 | 768 | 192 | 768 | 1536 | 3840 |
| 9 | 0 | 9 | 162 | 972 | 243 | 972 | 1944 | 4860 |
| 10 | 1 | 0 | 1 | 6 | 1 | 4 | 8 | 20 |
| 11 | 1 | 1 | 5 | 30 | 7 | 28 | 56 | 140 |
| 12 | 1 | 2 | 13 | 78 | 19 | 76 | 152 | 380 |
| 13 | 1 | 3 | 25 | 150 | 37 | 148 | 296 | 740 |
| 14 | 1 | 4 | 41 | 246 | 61 | 244 | 488 | 1220 |
| 15 | 1 | 5 | 61 | 366 | 91 | 364 | 728 | 1820 |
| 16 | 1 | 6 | 85 | 510 | 127 | 508 | 1016 | 2540 |
| 17 | 1 | 7 | 113 | 678 | 169 | 676 | 1352 | 3380 |
| 18 | 1 | 8 | 145 | 870 | 217 | 868 | 1736 | 4340 |
| 19 | 1 | 9 | 181 | 1086 | 271 | 1084 | 2168 | 5420 |
| 20 | 2 | 0 | 4 | 24 | 4 | 16 | 32 | 80 |
| 21 | 2 | 1 | 10 | 60 | 13 | 52 | 104 | 260 |
| 22 | 2 | 2 | 20 | 120 | 28 | 112 | 224 | 560 |
| 23 | 2 | 3 | 34 | 204 | 49 | 196 | 392 | 980 |
| 24 | 2 | 4 | 52 | 312 | 76 | 304 | 608 | 1520 |
| 25 | 2 | 5 | 74 | 444 | 109 | 436 | 872 | 2180 |
| 26 | 2 | 6 | 100 | 600 | 148 | 592 | 1184 | 2960 |
| 27 | 2 | 7 | 130 | 780 | 193 | 772 | 1544 | 3860 |
| 28 | 2 | 8 | 164 | 984 | 244 | 976 | 1952 | 4880 |
| 29 | 2 | 9 | 202 | 1212 | 301 | 1204 | 2408 | 6020 |
| 30 | 3 | 0 | 9 | 54 | 9 | 36 | 72 | 180 |
| 31 | 3 | 1 | 17 | 102 | 21 | 84 | 168 | 420 |
| 32 | 3 | 2 | 29 | 174 | 39 | 156 | 312 | 780 |
| 33 | 3 | 3 | 45 | 270 | 63 | 252 | 504 | 1260 |
| 34 | 3 | 4 | 65 | 390 | 93 | 372 | 744 | 1860 |
| 35 | 3 | 5 | 89 | 534 | 129 | 516 | 1032 | 2580 |
| 36 | 3 | 6 | 117 | 702 | 171 | 684 | 1368 | 3420 |
| 37 | 3 | 7 | 149 | 894 | 219 | 876 | 1752 | 4380 |
| 38 | 3 | 8 | 185 | 1110 | 273 | 1092 | 2184 | 5460 |
| 39 | 3 | 9 | 225 | 1350 | 333 | 1332 | 2664 | 6660 |
| 40 | 4 | 0 | 16 | 96 | 16 | 64 | 128 | 320 |
| 41 | 4 | 1 | 26 | 156 | 31 | 124 | 248 | 620 |
| 42 | 4 | 2 | 40 | 240 | 52 | 208 | 416 | 1040 |
| 43 | 4 | 3 | 58 | 348 | 79 | 316 | 632 | 1580 |
| 44 | 4 | 4 | 80 | 480 | 112 | 448 | 896 | 2240 |
| 45 | 4 | 5 | 106 | 636 | 151 | 604 | 1208 | 3020 |
| 46 | 4 | 6 | 136 | 816 | 196 | 784 | 1568 | 3920 |
| 47 | 4 | 7 | 170 | 1020 | 247 | 988 | 1976 | 4940 |
| 48 | 4 | 8 | 208 | 1248 | 304 | 1216 | 2432 | 6080 |
| 49 | 4 | 9 | 250 | 1500 | 367 | 1468 | 2936 | 7340 |
| 50 | 5 | 0 | 25 | 150 | 25 | 100 | 200 | 500 |
| 51 | 5 | 1 | 37 | 222 | 43 | 172 | 344 | 860 |
| 52 | 5 | 2 | 53 | 318 | 67 | 268 | 536 | 1340 |
| 53 | 5 | 3 | 73 | 438 | 97 | 388 | 776 | 1940 |
| 54 | 5 | 4 | 97 | 582 | 133 | 532 | 1064 | 2660 |
| 55 | 5 | 5 | 125 | 750 | 175 | 700 | 1400 | 3500 |
| 56 | 5 | 6 | 157 | 942 | 223 | 892 | 1784 | 4460 |
| 57 | 5 | 7 | 193 | 1158 | 277 | 1108 | 2216 | 5540 |
| 58 | 5 | 8 | 233 | 1398 | 337 | 1348 | 2696 | 6740 |
| 59 | 5 | 9 | 277 | 1662 | 403 | 1612 | 3224 | 8060 |
| 60 | 6 | 0 | 36 | 216 | 36 | 144 | 288 | 720 |
| 61 | 6 | 1 | 50 | 300 | 57 | 228 | 456 | 1140 |
| 62 | 6 | 2 | 68 | 408 | 84 | 336 | 672 | 1680 |
| 63 | 6 | 3 | 90 | 540 | 117 | 468 | 936 | 2340 |
| 64 | 6 | 4 | 116 | 696 | 156 | 624 | 1248 | 3120 |
| 65 | 6 | 5 | 146 | 876 | 201 | 804 | 1608 | 4020 |
| 66 | 6 | 6 | 180 | 1080 | 252 | 1008 | 2016 | 5040 |
| 67 | 6 | 7 | 218 | 1308 | 309 | 1236 | 2472 | 6180 |
| 68 | 6 | 8 | 260 | 1560 | 372 | 1488 | 2976 | 7440 |
| 69 | 6 | 9 | 306 | 1836 | 441 | 1764 | 3528 | 8820 |
| 70 | 7 | 0 | 49 | 294 | 49 | 196 | 392 | 980 |
| 71 | 7 | 1 | 65 | 390 | 73 | 292 | 584 | 1460 |
| 72 | 7 | 2 | 85 | 510 | 103 | 412 | 824 | 2060 |
| 73 | 7 | 3 | 109 | 654 | 139 | 556 | 1112 | 2780 |
| 74 | 7 | 4 | 137 | 822 | 181 | 724 | 1448 | 3620 |
| 75 | 7 | 5 | 169 | 1014 | 229 | 916 | 1832 | 4580 |
| 76 | 7 | 6 | 205 | 1230 | 283 | 1132 | 2264 | 5660 |
| 77 | 7 | 7 | 245 | 1470 | 343 | 1372 | 2744 | 6860 |
| 78 | 7 | 8 | 289 | 1734 | 409 | 1636 | 3272 | 8180 |
| 79 | 7 | 9 | 337 | 2022 | 481 | 1924 | 3848 | 9620 |
| 80 | 8 | 0 | 64 | 384 | 64 | 256 | 512 | 1280 |
| 81 | 8 | 1 | 82 | 492 | 91 | 364 | 728 | 1820 |
| 82 | 8 | 2 | 104 | 624 | 124 | 496 | 992 | 2480 |
| 83 | 8 | 3 | 130 | 780 | 163 | 652 | 1304 | 3260 |
| 84 | 8 | 4 | 160 | 960 | 208 | 832 | 1664 | 4160 |
| 85 | 8 | 5 | 194 | 1164 | 259 | 1036 | 2072 | 5180 |
| 86 | 8 | 6 | 232 | 1392 | 316 | 1264 | 2528 | 6320 |
| 87 | 8 | 7 | 274 | 1644 | 379 | 1516 | 3032 | 7580 |
| 88 | 8 | 8 | 320 | 1920 | 448 | 1792 | 3584 | 8960 |
| 89 | 8 | 9 | 370 | 2220 | 523 | 2092 | 4184 | 10460 |
| 90 | 9 | 0 | 81 | 486 | 81 | 324 | 648 | 1620 |
| 91 | 9 | 1 | 101 | 606 | 111 | 444 | 888 | 2220 |
| 92 | 9 | 2 | 125 | 750 | 147 | 588 | 1176 | 2940 |
| 93 | 9 | 3 | 153 | 918 | 189 | 756 | 1512 | 3780 |
| 94 | 9 | 4 | 185 | 1110 | 237 | 948 | 1896 | 4740 |
| 95 | 9 | 5 | 221 | 1326 | 291 | 1164 | 2328 | 5820 |
| 96 | 9 | 6 | 261 | 1566 | 351 | 1404 | 2808 | 7020 |
| 97 | 9 | 7 | 305 | 1830 | 417 | 1668 | 3336 | 8340 |
| 98 | 9 | 8 | 353 | 2118 | 489 | 1956 | 3912 | 9780 |
| 99 | 9 | 9 | 405 | 2430 | 567 | 2268 | 4536 | 11340 |
Now we could look for the number that coincides exactly with the number of squares or triangles in a polyominoes or polyiamonds set. I suggest the shapes below, without to guarantee the existence of a solution. However I'm optimist because no parity problems are present.
Hexominoes
Cube of line 23 (if you don't use the cross)
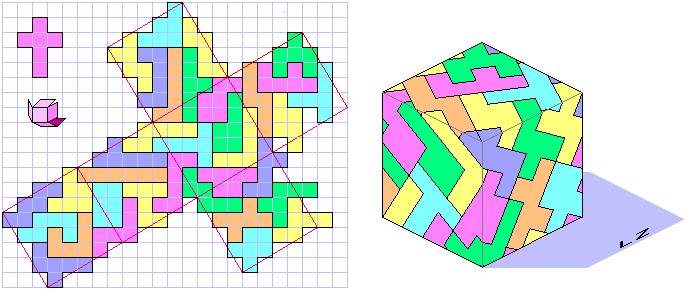
My solution
Hexominoes + Pentominoes
Cube of line 33 (35x6+12x5=270 exactly)
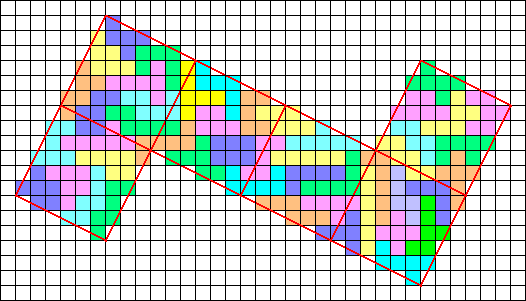
Sept 2001 - Solution by Alessandro Fogliati
Fractal
Cube covered by 6 fractals on a grid of infinite number of squares.

Sexominoes
The 6 full-sexed Sexominoes cover the cube nr. 10 exactly (solution)
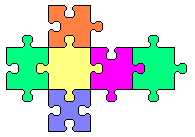
The 24 one-side Sexominoes cover the cube of line 20 exactly (solution)
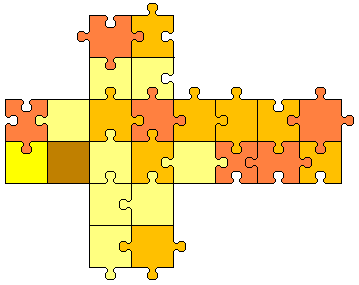
Sexominoes Number Five
Sometime my problem is to name the new polyforms: in this case I inspired by "Chanel nr.5" and "Mambo nr.5".
They are the 120 Order 5 squared flippable Polysexes. They cover the cube nr.22 exactly. (We must work with this interesting tile, also on the plane! I had supposed his existence some months ago, but it passed unnoticed. They are 120, that is a wonderful number for a geometric puzzle! Click here if you want to see all the Sexominoes Number Five.)
Sept 2001 - Solution by Alessandro Fogliati
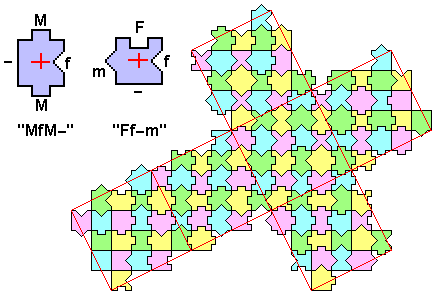
Tubominoes
The 30 two Flanges for edge Tubominoes cover exactly the cube nr.11. Do you want to minimize or to maximize the number of tubes? (I think it's a hard problem)
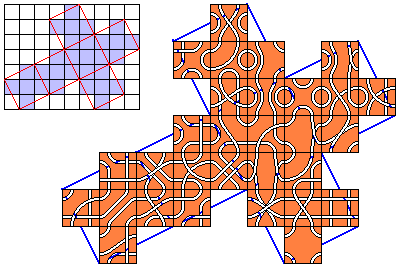
Polyarc
Here there are the 5 Tetrominoes with the 7 Biarc and the 22 Triarc by Henri Picciotto for a total of 60 squares! Do you want to cover the cube nr.21? I think it's possible.
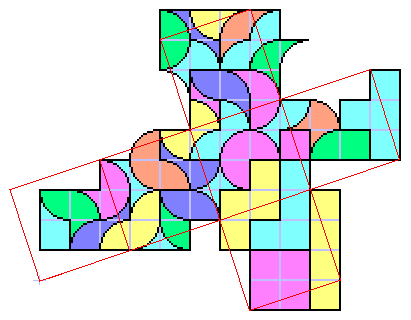
Sept 2001 - Solution by Alessandro Fogliati
.When I have seen the Picciotto's Page, I drew immediately the 24 Tri-Arc-iamonds.. I think they are nice but I don't know if they could cover the octahedron nr.30 (24x3=72 exactly).
Tiling
Sometime it isn't easy to tile a cube by a polyomino.
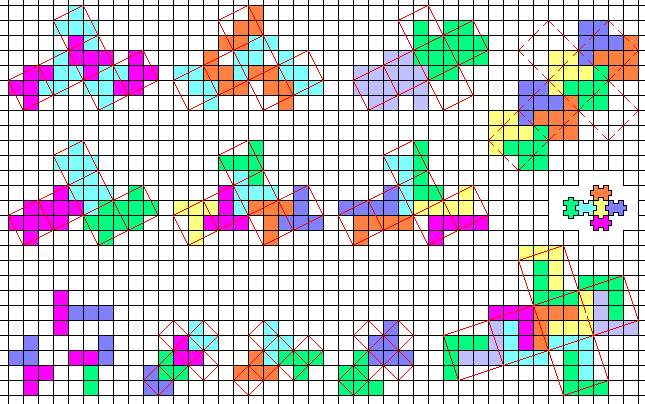
Many Polyominoes can to tile a cube area. The Domino and each Triomino tile the elementary cube. The cube nr.1 (12 squares) is tiled by a Triomino, a Tetromino and a Hexomino. Many Pentominoes (not all!) tile the cube nr.11 (30 squares) that is tiled also by a 10-omino and a 15-omino. The cube nr.2 (48 squares) is tiled by 2-3-4-6-8-12-16-24-ominoes! Perhaps it's not easy to tile the cube nr.21 (60 squares) with a Hexomino. The Sexomino "FMFM" tiles all the cubes.
Hexiamonds
Tetrahedron of line 12 and Octahedron of line 30
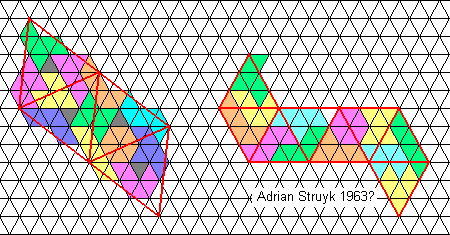
At left a solution by Alessandro Fogliati
Order 8 Isoperimetric Polyiamonds
Tetrahedrons of line 8 (exactly) and line 44 (with 4 holes)
You could find the Isoperimetric Polyforms on The Poly Pages by Andrew Clarke.
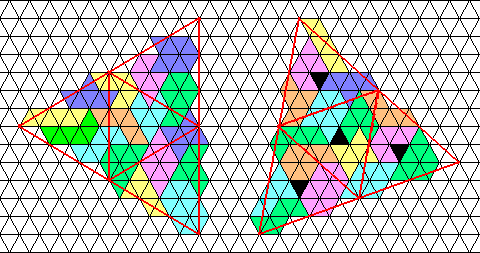
Sept 2001 - Solution by Alessandro Fogliati
Eptiamonds
Octahedron of line 31 exactly
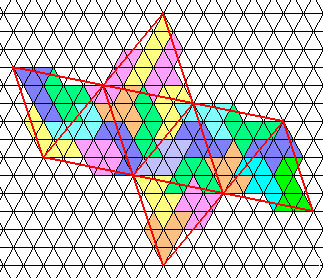
Sept 2001 - Solution by Alessandro Fogliati
Eptiamonds + Hexiamonds
Icosahedron of line 2 (12x6+24x7=240 exactly)
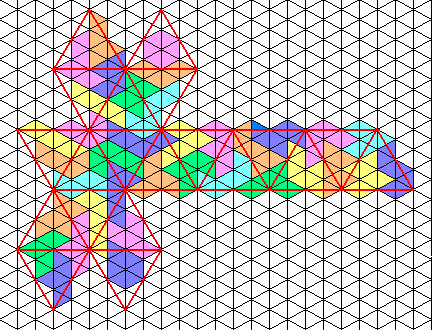
Sept 2001 - Solution by Alessandro Fogliati
Octiamonds
Tetrahedron of line 54 (66x8+4=532)
You could find many information about octiamonds on Mathpuzzle.com by Ed Pegg Jr.
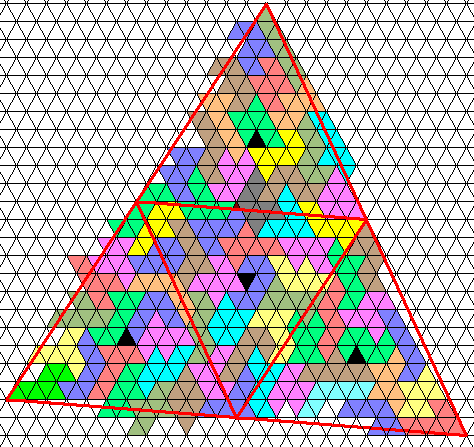
Sept 2001 - Solution by Alessandro Fogliati
Sexiamonds
The 4 Order 2 Triangular Polysexes cover the tetrahedron nr.10

Solution
Apartheid
These are the Order 14 two-side Triangular Polysexes. They are obtained coloring with 7 colors the 4 forms below. Each edge could be colored with a different color. The complete set has 560 pieces [see Chris Hartman's email]. The rules of the apartheid (terrible!) impose that only the edges with the same color can to join. The set could cover exactly the Icosahedron nr.22.

I'll die before see the solution of this puzzle.
Any racial tolerance (red with yellow, etc.) facilitates the solution. (The tolerance does easy the things!). If you use only 3 colors, you obtain a set of 56 pieces that cover exactly the Octahedron nr. 11. The Order 7 two-side Triangular Polysexes could cover exactly the Tetrahedron nr.31.
Polyhexes & SexeHexeS
This could be an other chapter. The study below shows that regular hexagons can to cover a regular octahedron, but not a tetrahedron or an icosahedron. There are many combinations.
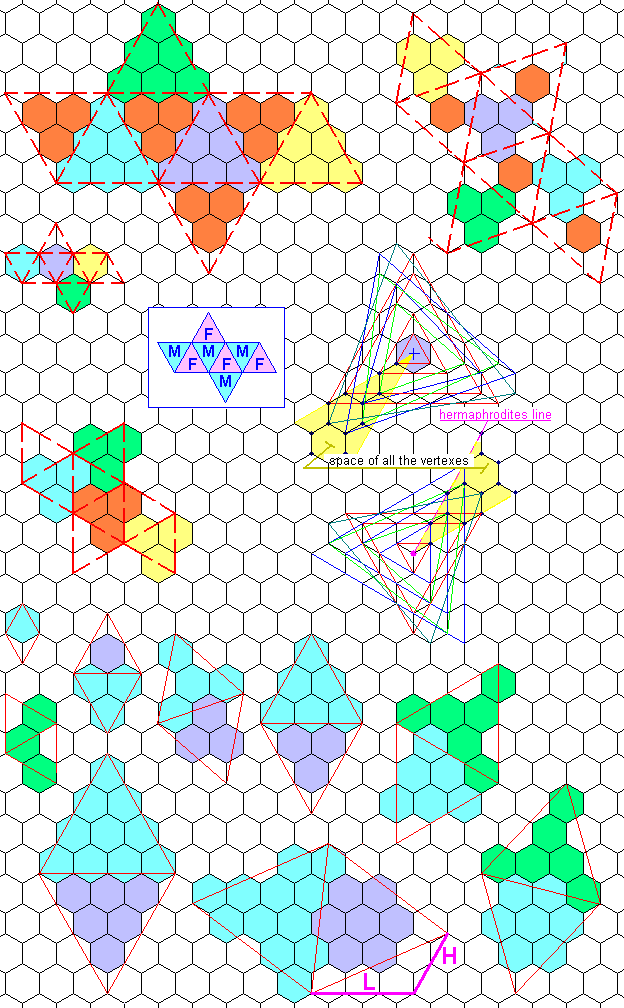
| Nr. | L | H | Hex on Octahedron |
| 1 | 1 | 0 | 4 |
| 2 | 1 | 1 | 12 |
| 3 | 2 | 0 | 16 |
| 4 | 2 | 1 | 28 |
| 5 | 2 | 2 | 48 |
| 6 | 3 | 0 | 36 |
| 7 | 3 | 1 | 52 |
| 8 | 3 | 2 | 76 |
| 9 | 3 | 3 | 108 |
| 10 | 4 | 0 | 64 |
| 11 | 4 | 1 | 84 |
| 12 | 4 | 2 | 112 |
| 13 | 4 | 3 | 148 |
| 14 | 4 | 4 | 192 |
| 15 | 5 | 0 | 100 |
| 16 | 5 | 1 | 124 |
| 17 | 5 | 2 | 156 |
| 18 | 5 | 3 | 196 |
| 19 | 5 | 4 | 244 |
| 20 | 5 | 5 | 300 |
| 21 | 6 | 0 | 144 |
| 22 | 6 | 1 | 172 |
| 23 | 6 | 2 | 208 |
| 24 | 6 | 3 | 252 |
| 25 | 6 | 4 | 304 |
| 26 | 6 | 5 | 364 |
| 27 | 6 | 6 | 432 |
| 28 | 7 | 0 | 196 |
| 29 | 7 | 1 | 228 |
| 30 | 7 | 2 | 268 |
| 31 | 7 | 3 | 316 |
| 32 | 7 | 4 | 372 |
| 33 | 7 | 5 | 436 |
| 34 | 7 | 6 | 508 |
| 35 | 7 | 7 | 588 |
| 36 | 8 | 0 | 256 |
| 37 | 8 | 1 | 292 |
| 38 | 8 | 2 | 336 |
| 39 | 8 | 3 | 388 |
| 40 | 8 | 4 | 448 |
| 41 | 8 | 5 | 516 |
| 42 | 8 | 6 | 592 |
| 43 | 8 | 7 | 676 |
| 44 | 8 | 8 | 768 |
| 45 | 9 | 0 | 324 |
| 46 | 9 | 1 | 364 |
| 47 | 9 | 2 | 412 |
| 48 | 9 | 3 | 468 |
| 49 | 9 | 4 | 532 |
| 50 | 9 | 5 | 604 |
| 51 | 9 | 6 | 684 |
| 52 | 9 | 7 | 772 |
| 53 | 9 | 8 | 868 |
| 54 | 9 | 9 | 972 |
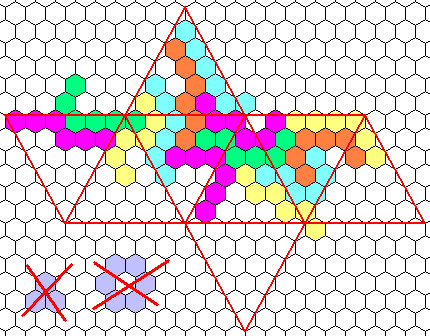
Tetrahexes
Octahedron of line 4 (my solution)
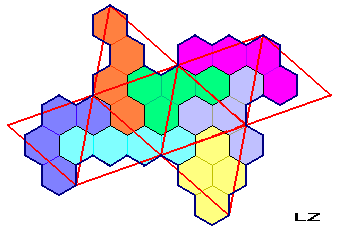
Order 6 Hexastrips
Octahedron of line 21 (24x6=144 exactly)
The Polystrips are an invention of Miroslav Vicher.
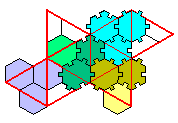
SexeHexeS
Do you want to solve the octahedron nr.2 with 12 of 13 full-sexed sexehexes? Or the octahedron nr.11 with 84/92 sexehexes?
_________________
First edition: Aug 15th, 2000 - Last revision: Sept 20th, 2001

|
HOME |
|
e-mail |
Download |
Links |
Chronicle |
|
PENTOMINOES |
|
More about pentominoes |
The cube |
3D pentominoes |
Maximizing |
|
POLYSEXES |
|
Sexominoes |
Xominoes |
Zucca's Puzzle |
Domino Puzzle |
SexCubes |
Dodecaculeus |
Tubominoes |
|
SEXEHEXES |
|
SexeHexeS For Sale |
More about SexeHexeS |
How we did it |
Other Sexehex Puzzle |
My Solution |
Reproduction |
|
POLYMULTIFORMS |
|
PolyEdges |
To cover a solid |
Fourier Series of a Square |
Order 13 Perfect Square |
Fibonacci Machine |



 Index
Index




