Maximizing
The young students of T.I.D. RONSE BELGIUM and their math teacher Odette De Meulemeester propose to maximize the area covered by the 12 pentominoes, which are joined with an edge at least. It's a nice puzzle and it isn't trivial. Try it.
I propose you to generalize the problem to all the polyforms!
Tetrominoes
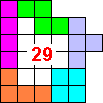
2 Aug 2000 - Livio Zucca - Maximum
One-side Tetrominoes (Tetris)
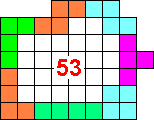
Is it the maximum?
Pentominoes
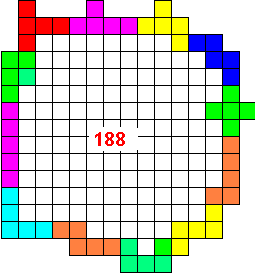
This is my 188-solution.
Hexominoes
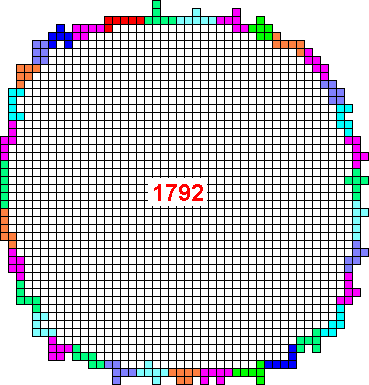
Oct 19th, 2000 - Francesco Zanchettin (frankyz)
Hexiamonds
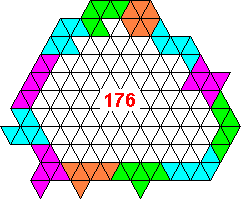
You could do better!
TetraCairos
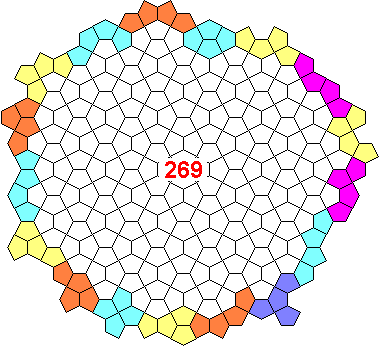
4 Aug 2000 - Mario Ricciardi
Tetrahexes
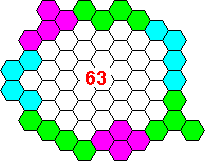
Could you do better?
TetraSquares
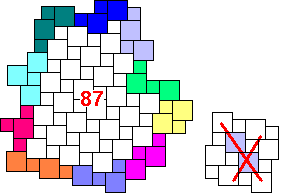
Could you do better?
Tetrabricks

Could you do better?
If you have a relative or absolute maximum about any polyform, send it to me: I'll publish it here with the date and your name.
_________________
Chronicle
Aug 3st, 2000 - Ed Pegg Jr: "These are known as Farm problems, where the polyform is used to make a fence. If you try to make two identical shapes with a large hole, to problem becomes even harder. Also, trying to make a symmetrical shape with the largest possible hole is quite hard."
Aug 4th, 2000 - Mario Ricciardi sent his Tetracairos 269-solution.
Aug 5th, 2000 - Rodolfo Marcello Kurchan: "Puzzle Fun number 4 of April 1995 is devoted to Pentominoes Farms."
Aug 8th, 2000 - Mario Ricciardi sent his Hexominoes 1788-solution.
Aug 16th, 2000 - Predrag Janicic (who talked me first about this problem) suggests to prove mathematically that those are true maximal values.
Aug 20th, 2000 - Dario Uri: [my translation]
"The problem of the maximal contained by the
pentominoes area is rather note, Victor Feser proposed it and
Donald Knuth (!) found the 128 (internal squares) solution first,
published then by Gardner. The Italian edition of Scientific American num.69 May 1974 pag.89 has a demonstration that 128 is the maximum.
The Journal of Recreational Mathematics vol.17 num.1 1984-85
pagg.75-77 has a generalization: if the
pentominoes could also touch only for the vertexes, then a 160 solution exists (internal squares), if the pieces could be not on the the greed, then there is a >161 solution."
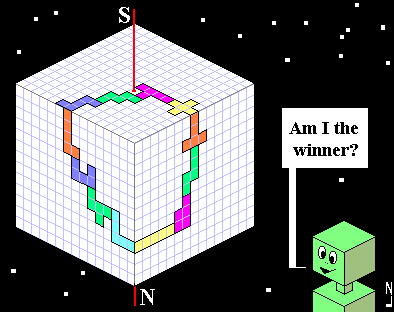
Sept 17th, 2000 - OB1-3D:
"My name is OB1-3D and I live on the planet 'Cubik'. Don't believe who say 128 is the maximum! Here there are bigger farms. Won't you discriminate me for my green skin?"
Oct 19th, 2000 - Francesco Zanchettin (frankyz) improves Mario's Hexominoes 1788-solution for 4 squares.
_________________
First edition: 2 Aug 2000

|
HOME |
|
e-mail |
Download |
Links |
Chronicle |
|
PENTOMINOES |
|
More about pentominoes |
The cube |
3D pentominoes |
Maximizing |
|
POLYSEXES |
|
Sexominoes |
Xominoes |
Zucca's Puzzle |
Domino Puzzle |
SexCubes |
Dodecaculeus |
Tubominoes |
|
SEXEHEXES |
|
SexeHexeS For Sale |
More about SexeHexeS |
How we did it |
Other Sexehex Puzzle |
My Solution |
Reproduction |
|
POLYMULTIFORMS |
|
PolyEdges |
Fourier Series of a Square |
Order 13 Perfect Square |
Fibonacci Machine |



 Index
Index




