Tiling The Plane
When does a piece tile the plane?
This is the question.
This is my work on the tiling problem. It wants to become a systematic study, but it isn't yet. It is open to external contributions. Errors are possible. I appreciate the corrections (also of my English :-). I'm happy when I receive an email.
The equilateral triangle, the square and the regular hexagon tile the plane. This is trivial:
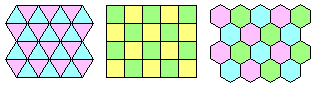
All the triangles and all the quadrilaterals tile the plane. This is easy but less trivial:

Irregular hexagons tile the plane with conditions. A sufficient condition is the parallele edges, an other one is two equal and parallele opposite edges:
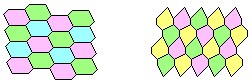
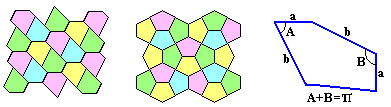
Also pentagons tile the plane. For example, at left you see "half hexagons". At right equilateral (not regular!) pentagons with two angles of 90°. A sufficient condition for a pentagon to tile the plane is to have two complementary angles (sum=180°) betwin two pairs of equal edges or to have two complementary consecutive angles:
There are pieces witch tile the plane and pieces witch don't tile the plane (Mr. Lapalisse). There are pieces witch tile the plane maintaining the same orientation as the Sexominoes below. There are pieces witch must to rotate as the Xominoes. There are pieces witch must to flip as the SexeHexeS or the PolyTriForms.
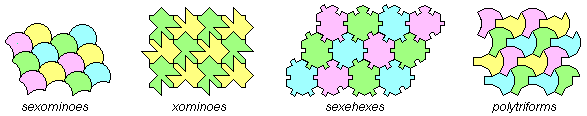
Many polyforms tile the plane. All the Octiamonds tile the plane. All the Pentominoes. All the PolyTriForms.
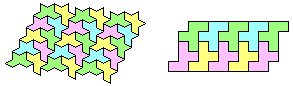
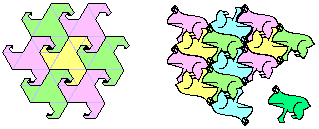
Also Fractals and a Frogs...
If we consider the irregular convex polygon tilings where the vertexes coincide, you could see easily below that only the triangle, the quadrilateral, the pentagon and the hexagon can tile the plane.
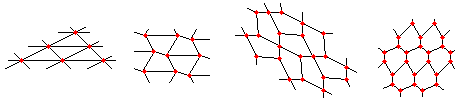
Demonstration:
In a convex polygon each angle is < Pi. Then each knot is minimum triple. A polygon with n edges confina on n identical polygons. The sum of internal angles and the angles confinanti don't must to superate 2*n*Pi. The risult of disequation is n<=6:
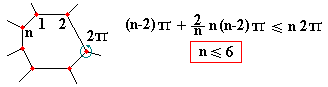
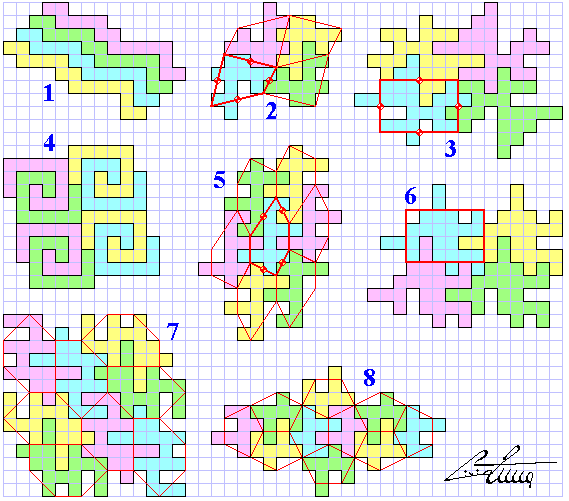
We can to deform now each polygon to obtain very irregular figures, or artistic, if you are able:
| Nr. edges | Regular | Irregular convex | Concave |
| 3 | YES | ALWAYS | - |
| 4 | YES | ALWAYS | ALWAYS |
| 5 | NO | WITH CONDITIONS | WITH CONDITIONS |
| 6 | YES | WITH CONDITIONS | WITH CONDITIONS |
| 7 + | NO | NEVER | WITH CONDITIONS |
_________________
It isn't trivial!
First edition: Jun 12th, 2000 - Last revision: Oct 20th, 2003




 Index
Index




