PoliMultiForms4

PolyMultiForms
August 2001 edition

Click here to see the May 2000 edition. (PentaSlimbes, PolyBiSquares, PolySquareRhombi, PolyBricks, DualOctagonSquares, FourStars&Pentagons, HexagonRhombi, DualStarHexSquares, PolyTriForms, TetraFrogs)
Click here to see the Aug 2000 edition. (Hexagon by Zucca's Puzzle, PolyDoms , Big Pizza, Kites & Bricks, DomSlicedPolyominoes, PolyPenroses, Sexominoes Number Five, Poly-Arc-Iamonds, More about PolyCairos)
Click here to see the Mar 2001 edition. (PolyBricks solutions, Break & Paste Polyforms, PolyWorms, TetraSticks)

News

Pierpaolo Bernardi counted the number of solutions of the Sexominoes 6x4 puzzle. They are 147,928. See here the troubled story (Italian).

Mark Stubbings finds the final solution of the Zucca's Puzzle with 1355 pieces and the neuter edge. You could download a colored image here (740x1300 pixels - 73KB).

Alessandro Fogliati solved a lot of things:
- The Domino Puzzle with perimeter=10.
- The 8x8 square puzzle of TSOB.
- The 120 Sexominoes Number Five 12x10 rectangle.
- The minimizing of the pipes number of the Tubominoes.
- The 120 Sexominoes Number Five cover a cube.
- 5 Tetrominoes + 7 Biarc + 22 Triarc by Henri Picciotto cover a cube.
- The Octiamonds cover a tetrahedron.
- The Heptiamonds cover a octahedron.
- The Isoiamonds(8) cover two tetrahedrons.

I solved:
- The 36 PentaSquares in a simmetrical box.
- The Hexominoes cover a cube with edge=sqr(34)

PentaElly story

Once upon a time there was an ellipse. When R/r became sqr(3) he was able to arrange this crossed lattice and was tangent to the other ellipsis:

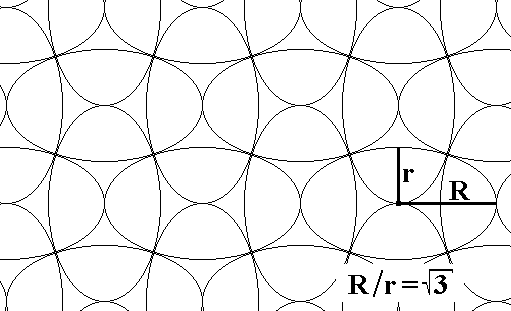
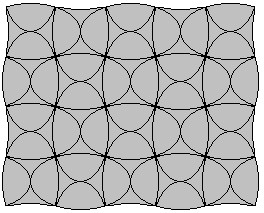
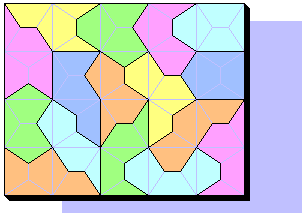
The forms joined five to five and 16 PentaElles had born:

Will they be able to cover the shape below?

I built a software for solving polyminoes problems which uses the Gerard Putter Java Engine. The merit is all of Gerard, but with my SW, it is more easy. You could design the polyminoes and the shapes. It produces a HTML file with all the parameters for the Gerard's Engine.

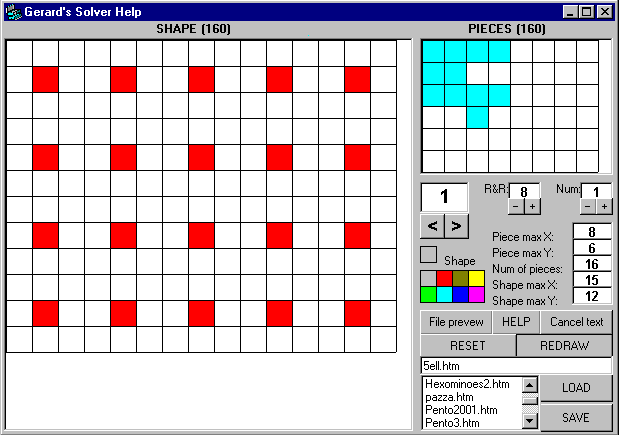
It runs on MS Windows95 or better with Internet Explorer 5.0 or better. You could download the compact form here [67KB]. It's possible you don't have a DLL file. In this case you must to download the complet setup program here [1.5MB].

It was then necessary to codify the pieces as polyominoes:

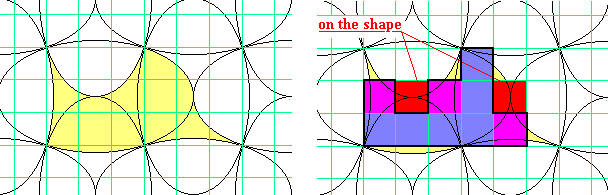
It was easy fixing the central red square on the shape. The Gerard's Engine produced the solution:

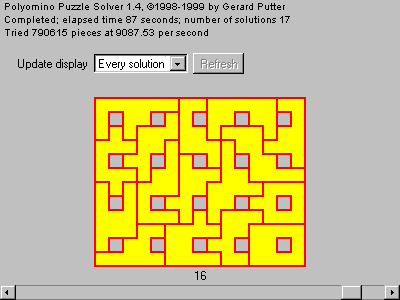
And I have redrawn it so:

If you rectify the edges, you get polyforms which could be inserted into an exact rectangle:

In this case the lattice remember us the Pentagonal Cairo Tasselation, crossed with a square grid. This puzzle has 17 different solutions.

Sept 4th, 2001
Brendan Owen did some counts:

Order	Nr.PolyEllys
1	2
2	2
3	4
4	8
5	16
6	36
7	84
8	206
9	504
10	1260
11	3168
12	8085
13	20738
14	53639
15	139302

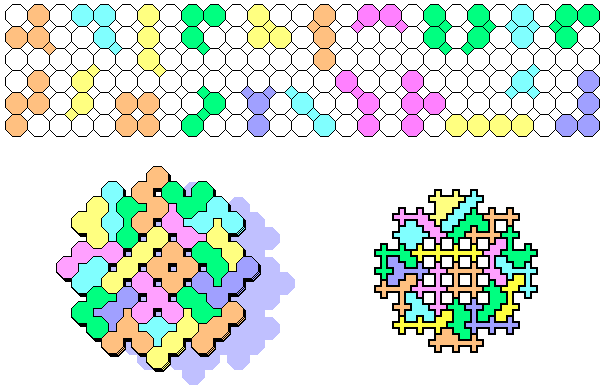
... and he has found this solution for the 28 one-side pentellys:

He has transformed them into poly-checkered-mini-tans on checkered triangle grid. See here his original solution.

_________________

PolyOctagonSquares

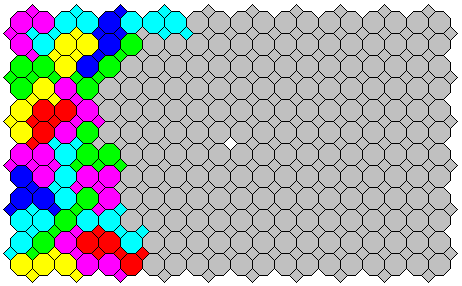
Below there are the 22 PolyOctagonSquares defined as:

Nr. of octagons + nr. of squares = 4

They can fit into this shape. At right the solution by coding the poliforms as polyominoes on Gerard's Solver.

Do you remember the 80 TriOctagonSquares (where nr. of octagons = nr. of squares = 3) which Brendan Owen calculated? I think it's the time for a solution :o)
I'll publish the first. Below a possible shape: