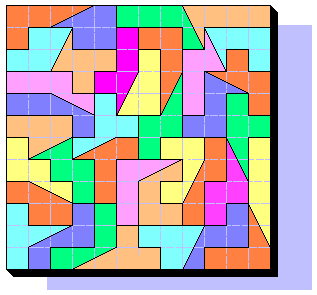
Roel Huisman has found 36 pieces if you remove half a Domino (with one cut) from the Pentominoes. He has also produced this 12x12 fantastic square. He named them DomSlicedPentominoes.

I have redrawn the 36 pieces for me and for the collectors here. The position of the last 5 pieces is 'casual'. The Roel's paternity is indisputable.

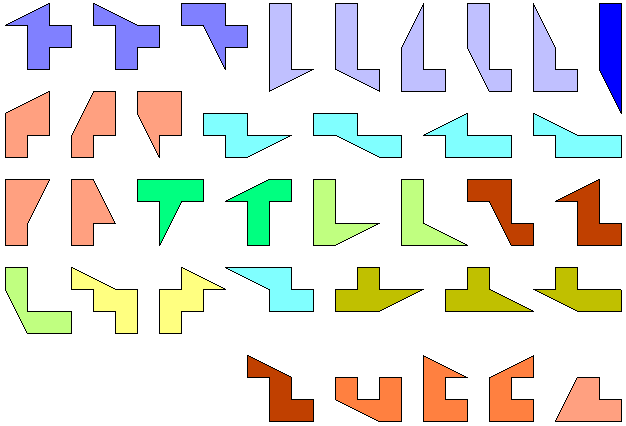
It's possible that the name of these polyforms is not definitive. The Anglophones like the short names. Could be 'Pent' the correct one? (Pent=4/5Penta)

Now we do a step backward:

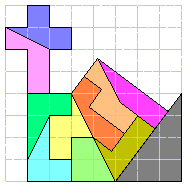
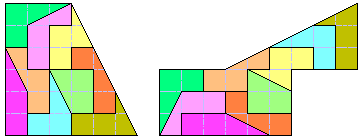
They are ten. One piece has parity problems, it's sufficient to proof that is not possible to cover 5x6 rectangle. Two sets can to cover a 12x5 rectangle with piece symmetry. I used a set and the 3x4x5 triangle to build the church below. The title of this picture is:

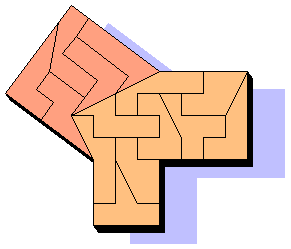
Yes, because also the Pents, as the PolyDoms, could do the 'jump of the grid':

I have the sensation that we'll talk about them next days.

Sep 18th 2000 - I solve two triplication problems of DST. Not all DST can be triplicated with one set. However we must to use the 9 even pieces.

Sep 19th 2000 - Roel Huisman heats the motors and finds a classic 6x10 Pentamino rectangle covered by 2 DST sets....

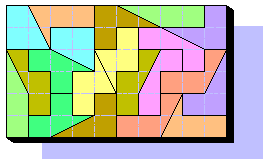
... and he solves many other problems that remenber us typical historical pentomino shapes:

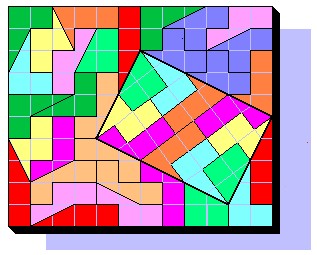
Sep 20th 2000 - Finally , with 4 DST sets, I can to show the possibility of the irrational jump of rational poliforms (rational because DST = 3/4 tetromino, irrational because the 'island' grid is rotated of arctan(3/4) that is a irrational number and its edge is multiple of SQR(5) that is irrational too.).
The 'island' is 2SQR(5) x 3SQR(5) = 30, multiple of a SQR(5) x 2SQR(5) domino (see here the Doms' island conjecture). The principal rectagle is 12x10 = 120 = 30x4.

Sep 21th 2000 - Mario Ricciardi send me this interesting

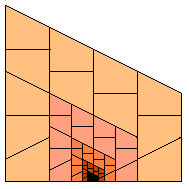
Sep 21th 2000 - Ed Pegg Jr suggests to look for Pentomino-hole in a 13x13 DomSlicedPentominoes square. It could be possible!

Sep 23th 2000 - Roel Huisman find this DST 7x22 rectangle with 2 SQR(5)*SQR(5) holes.

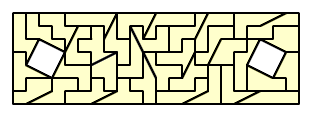
Sep 24th 2000 - Roel Huisman send:
"Two more scaled-tetrominoes with the DSP's.....somebody help me with the last one please!"

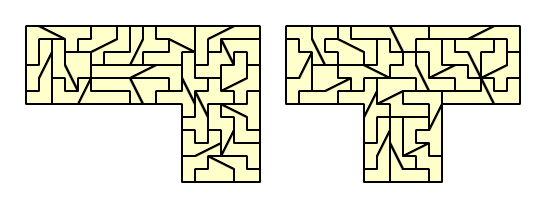
Sep 25 th 2000 - Alexandre Owen Muñiz send me:
"Here's a neat little puzzle I found, playing around with the dom-sliced tetrominoes:
Find a set of 5 different hexominoes, such that each can be split with a single cut into at least two different pairs of dom-sliced tetrominoes, and such that, if the right cuts are chosen, all 10 dom-sliced tetrominoes are created. In the solution I found, there is a unique set of cuts that works. I think my solution for the hexomino set is also unique, but I may have missed a usable hexomino."