PolyMultiForms - August 2000 Appendix
Click here to see the May-June edition.
Click here to see the 2001 edition.
Please see also the Zucca's Puzzle Sep 11th up-date.
Wonderful!!!
Ed Pegg Jr on his Prize Page writes:
"Prize Puzzle. A $100.00 prize will go to the first solver of Livio Zucca's Big Pizza Puzzle - whether you solve the puzzle or prove it impossible."
(See below)
Surprise!
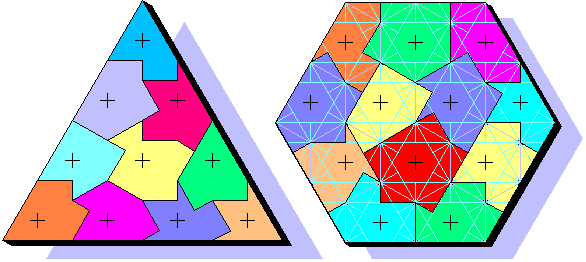
Have you seen that it's possible to build perfect equilateral triangles and hexagons with the pieces of Zucca's Puzzle?
 CONTEST
CONTEST 
I offer a free SexeHexeS set

to the solver who will find before midnight of Christmas 2001 (12/25/2001) the biggest (= which has more pieces) perfect equilateral triangle or hexagon. The solver must to send an ascii text for solution testing, in the form " x, y, piece", rows number = pieces number. Example:
30, 31, mmFMMF
31, 32, F-M-mm
32, 31, Mf---M
31, 30, F-FFf-
30, 29, -MMM-F
29, 30, m--fFf
...
See also the rules and the particulars on Zucca's Puzzle.

This grid could help you. If you haven't software, you can to download the bit-map grid and open it with Paint of Windows. Or you can to download my Drawing Machine for Windows [1.417KB]. You can to see here a true sample of a 75 pieces hexagon in graphic version and in text version.
Write me if you need explanations.
Jun 6.th, 2001 - You could see below the big hexagon by Mark Stubbings. Will he the winner?
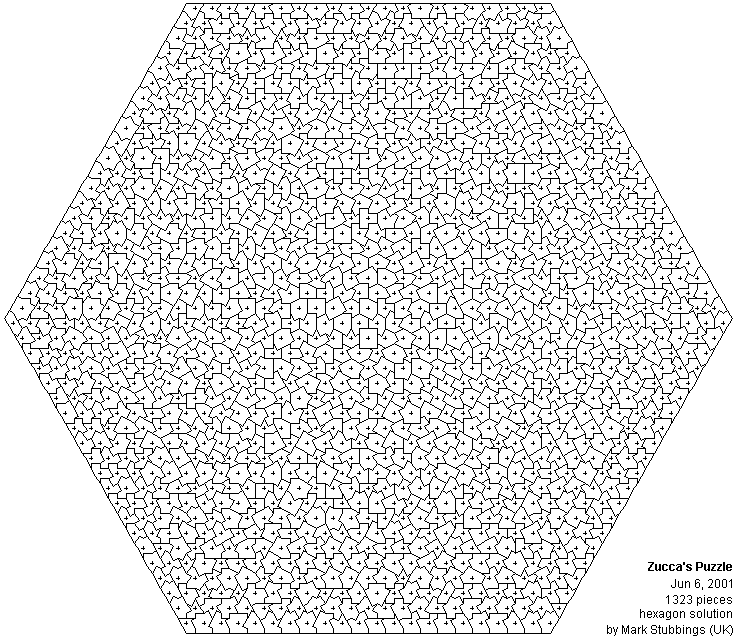
__________________
After a democratic election, we call these polyforms:
PolyDoms
alias PolyWeiHwaEdes, PolyRights, PolyDeminoes, PolyHemiDominoes, PolyPythagoras, PolyPinwheels. Andrew Clarke named PolyDoms these polyforms.
(Dom = 1/2 Dom-ino (!)) - Here the vote results.
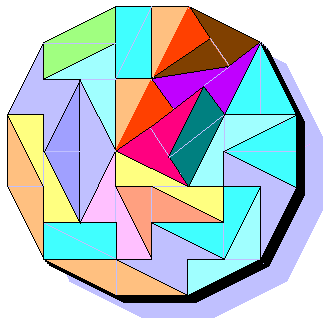
Two sets of DiDoms cover a dodecagon. This fantastic solution is by Brendan Owen. Notice at top-right how a domino-form island has surrounded by a sea of an other grid. Without 'jump of the grid' there is not solution!
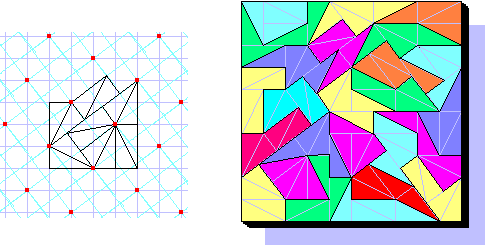
PolyDoms double-grid and a 10x10 square covered by a TetraDoms subset.
Here I must tell a story with my bad English:
Some days ago, Ed Pegg Jr. took one week's holiday. Before to go away, he quickly invented a puzzle to hold us busy. He wrote on his web-page:
"The below figure is a famous Pythagorean illustration of the 3-4-5 triangle. Can the whole thing be divided into identical triangles? If yes, which is the minimum?"
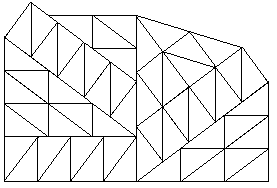
While Ed spent his holidays, any poor men searched the solution: somebody found 33600 triangles solution, others 5376, Joe Logic, Al Zimmermann and I 1344. Joseph DeVincentis found a brilliant 336 solution. The day after, with a 'brilliant and exact' :o) mathematical proof, I demonstrated that the Joseph's solution is the absolute possible minimum. Some hours later Wei-Hwa Huang found an incredible solution of 56 triangles, where the triangles are not congruent with the main 3x4x5 (!). Ed (old fox) announced the news without give the solution: that night I didn't sleep!
For discovering the solution, I drew the square double-grid aloft at left. The second grid, identical to first, is rotated of arctg(3/4). A triangular tile of 1x2 (area=1) can change the grid on the red points.
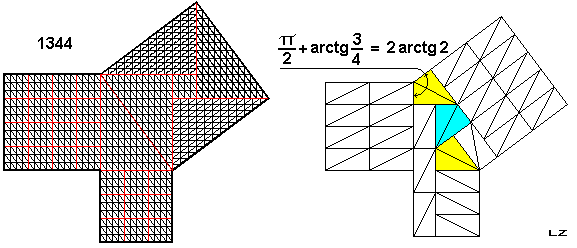
My first and my last solution. Sincerely I found the last only because I knew that it exist.
Finally I saw the solution, probably equal to Wei-Hwa Huang solution. (While I write, I don't know). I drew the polyforms on this double-grid . I told the story to explain why I called PolyWeiHwaEdes these poliforms initially.
We must to study them yet, but we can say that they are interesting, because the tiling of the elementary triangle can be non-periodic and the shapes can be rectangular or squared or polygonal. The solutions non-easy.
Obviousely you can also cover the Ed's puzzle!
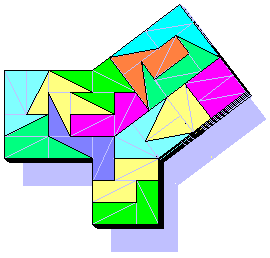
(Now Ed Pegg Jr. builds for selling a set of 2x13 DiDoms + 4 Doms = 56 and Brendan Owen found first a solution.)
But the real novelty of this tiling is the "jump of the grid"!!! Observe the figure below: The central green pieces are on the red grid. With a jump of one grid, the pink pieces have an other orientation, on the grey horizontal and vertical grid.

The trick could continue to the infinity with a third grid, rotated on the second, and so on. The peripheral blue pieces are on the green grid. The rotation is of arctg(3/4), which is an irrational number! Then you can get, to infinity, all the orientations, and when I say ALL, I say ALL! And this is a novelty. I don't know tessellations which do it, not even those of Sir Roger Penrose.
27th Aug 2000 David Eppstein write me:
'Congratulations, you've rediscovered the pinwheel tiling.'
OK, OK, we have exaggerated. We didn't invent anything, we have only discovered that polyforms of right triangles may be interesting
because they change orientation. And probably they are a good new challenge for the computer solvers.
27th Aug 2000 Brendan Owen write:
'The property of it having all orientations is the same for most other right angled triangles. The idea can easily be generalized... You could call the general form polyrights.'
Yes, it is. In the example below a 2x3 triangle jump on a 5x12 grid.
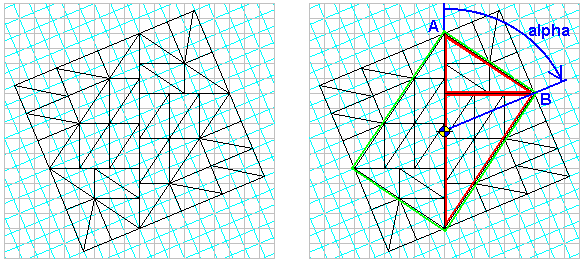
2atan(3/2) = PI+atan(5/12) and the generalization.
At right the proof that all the right angled triangles with rational catheti-ratio can to tile the plane jumping on different grids:
1) build the red congruent triangles with the common cathetus = least common multiple of catheti.
2) build the green rectangle = red triangles x 2.
3) using the baricenter of the rectangle, rotate the grid of alpha, from vertex A to vertex B.
An interesting conjecture: an island of Doms or PolyDoms can to have only a Domino or a PolyDomino form with edge = SQR(5), all the PoliDominoes without holes or with PolyDomino holes can to be an island. An island is an agglomeration of Doms on a square grid surrounded by Doms on one only other grid with different orientation.
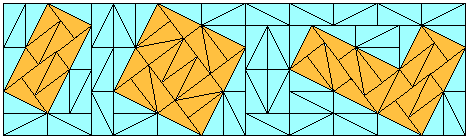
If you use a 3-4-5 triangle or other triangle with rational hypotenuse/catheti ratio (for example 5-12-13) you'll obtain a very complex tiling:
However I think that we could begin to build polyforms with the hemi-dominoes. These are the 13 possible DiDoms:
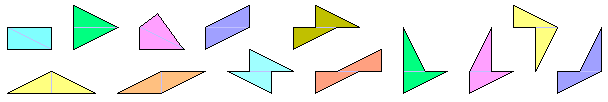
Do you want to cover my dog figure? It's not for children.
Notice: the back of the head has 4/3 inclination.
Brendan Owen found the solution using 'human and artificial intelligence' (but not clicking the dog picture as you can do :o). He thinks (I also) that it is unique.
Why a double set of DiDoms?
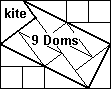
In a 13 DiDoms set there is one only 'kite'. This piece forces the jump of the grid, but a multiple of 10 Doms are necessary to form an island. If a Dom is supplyed by the kite, 9 remain that is impossible to cover with DiDoms:
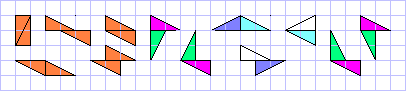
If the kite is left out, the 'normal' 12 pieces have a parity problem and they can't cover a rectangle or other regular shape (not even a cube):
With 2 sets each problem disappears. The Brendan's solution of the dodecagon is a proof. Also my solution of the 4x13 rectangle:
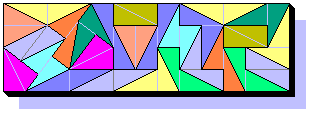
Ed Pegg Jr. adds 4 Doms to cover the Pythagorean figure for a total of 56 Doms. I propose you the hexagon below with his set. Notice the 4 symmetrical jumps of the grid! Moreover, the 6 edges are integers.
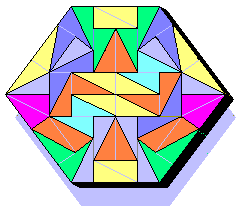
TriDoms
Here there is a set of 86 TriDoms. Is it possible to do any shape? If the geometry doesn't help us, I hope the fantasy does it.

Nothing gives me the proof that the Big Pizza below is impossible but, if it's possible, it's certainly very hard. (See also my feasibility study.).

Big Pizza - False solution
 CONTEST
CONTEST 
I offer a free SexeHexeS set

to the first Big Pizza solver.
Wonderful!!!
Ed Pegg Jr on his Prize Page writes:
"Prize Puzzle. A $100.00 prize will go to the first solver of Livio Zucca's Big Pizza Puzzle - whether you solve the puzzle or prove it impossible."
Also I offer the SexeHexeS set to the first person to prove that the construction is unfortunately impossible. Wow! Sponsors! Ed is an authority! If you want to contribute, I'm here!
Superior Order PolyDoms
August 28th I said: Warning: The principal rule for building superior order polyrights is: the polyform must to stay on the double grid, at top left of this page. I have some perplexity if to admit or not a piece as below that is drawn on two jumps of the grid. Without this tile, you can do a double jump however; with this tile you must do a near double jump. I suspend the judgment. Write me please.
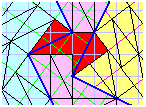
September 5th I thank all people that has written me about my perplexity. Particularly I appreciate and I use the advice of Mario Ricciardi and Brendan Owen. These the conclusions:
We could choose to extract the PolyDoms from a grid of horizontal dominoes...

or from a grid of bricks...

or from a grid of orthogonal dominoes. In the last case we get the 12 DiDoms without kite.
But our purpose is to build interesting polyforms that test 'human and artificial brains'. Than we chose to extract the PolyDoms from "each variants of the Doms' grid that can be closed by one only orthogonal grid".
Below you have an example and you can see all the possible 10 TetraDoms that force a near double jump of the grid:
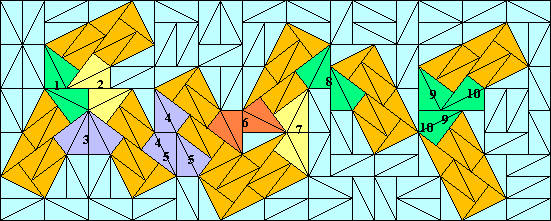
And here a HexaDom forces a possible near triple jump (4 grids):
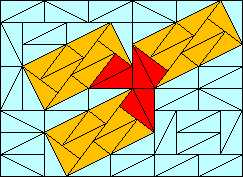
Maybe a TetraDom can force a double jump of the grid, a HexaDom can force a triple jump of the grid, a 2N-Dom can force a N-jump of the grid. But this is only a conjecture.
Kites & Bricks
(Kite is here a DiDom and Brick = Domino)
Last an interesting variant for PolyBiForms making: the bricks and the kites:
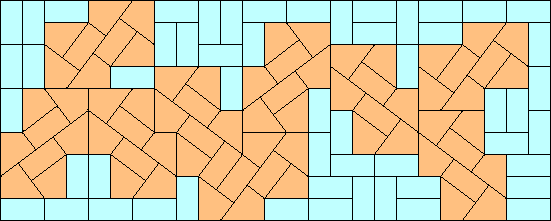
It's possible to cover a 10x10 square with 50 bricks, it's trivial. Also to insert 6 kites and 44 bricks it's easy. 28 kites and 22 bricks are less easy. Do you want to try? Is 28 the maximum number of kites ?
DomSlicedPolyominoes
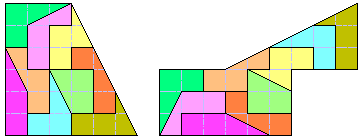
Roel Huisman and Andrew Clarke worked on Pentominoes cutting a Dom. The DomSlicedPolyomino was born. We dedicate a new page to them.
_________________
PolyPenroses
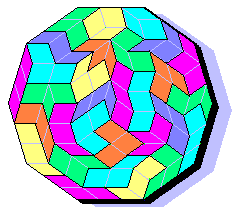
TriPenroses 30/55 subset
Why not? Sir Roger Penrose invented this fantastic a-periodic or quasi-periodic tessellation with only two particular rhombuses. I had the suspect always that Penrose is a pseudonym: Pen(tagonal)Rose :o). I hope to be not 'blasphemous' if I use his rhombuses to build the set below.
I suggest try to cover a shape as below. Try first a false-solution to test the number of 'slim and fat' rhombuses.

Many PolyPenroses can to do non-periodic tiling. Increasing the order, the game becomes non-trivial. Try please.

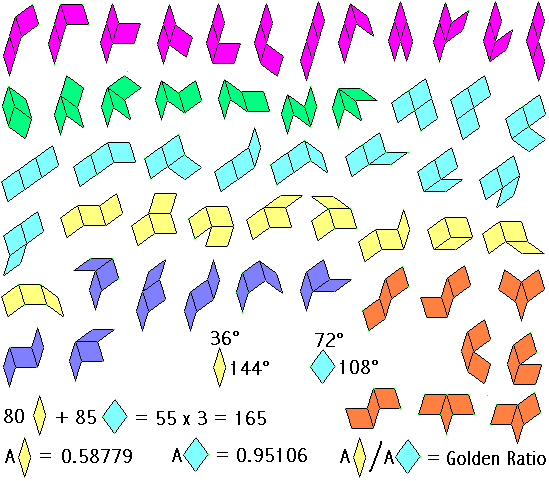
Sexominoes Number Five
Sometime my problem is to name the new polyforms: in this case I inspired by "Chanel nr.5" and "Mambo nr.5".
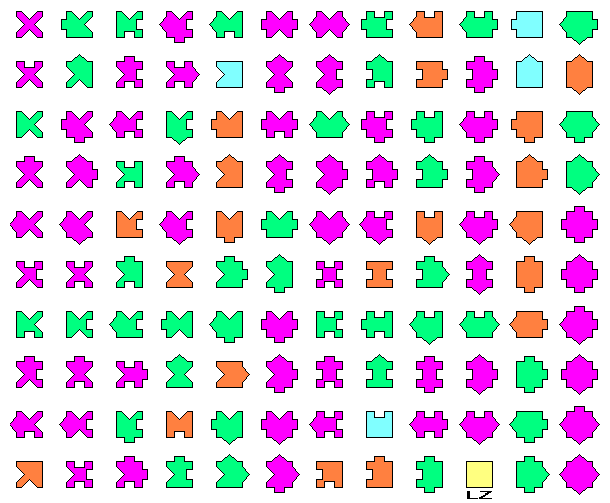
They are the 120 Order 5 squared flippable Polysexes. I supposed his existence some months ago, but it passed unnoticed. 120 is a good number for a geometric puzzle: 12x10, 6x20, 8x15, 11x11 with a central hole, etc. Don't confuse them with the Xominoes. See also 'To cover a solid'.
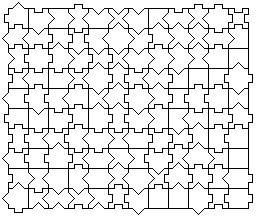
This is the first 10x12 solution by my Darwin Machine. Is it possible to do a rectangle with straight edges? I bet it is.
Aug 19th, 2001
Alessandro Fogliati finds the solution below:
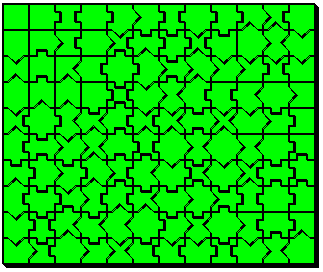
Poly-Arc-Iamonds
I like very much the Polyarc by Henri Picciotto. I have drawn here the Tri-Arc-Iamonds. Are nice, don't you think? They look like bat wings. They cover 72 triangles as the Hexiamonds. Could they cover the shapes that are covered by the Hexiamonds?

More about PolyCairos
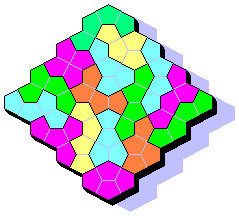
This beautiful TetraCairos' solution is of Brendan Owen, published on line by Ed Pegg Jr. (Ed has also some collections for sale). It is a solution with a 16/17 subset. However a symmetrical solution with all the 17 TetraCairos isn't possible for parity problems. Below you could see a parity study for the 55 PentaCairos:

This suggests to try to cover fantasy shapes, as the kite below, or better.
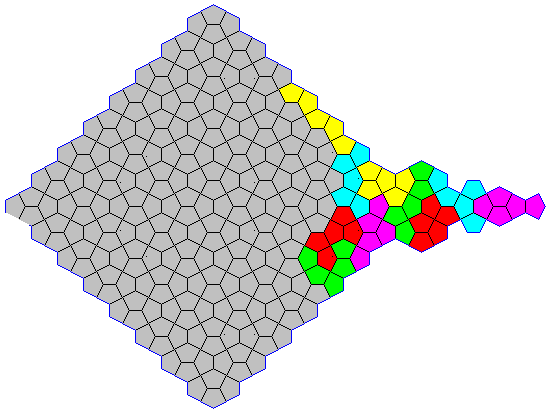
I suggest also to tile the plane with PolyCairos. Any don't tile the plane (red). Any seems to don't tile. Some we must to flip and to rotate.

_________________
It isn't trivial!
First edition: May 18th, 2000 - Last revision: Apr 30th, 2001 (Ed prize)

|
HOME |
|
e-mail |
Download |
Links |
Chronicle |
|
PENTOMINOES |
|
More about pentominoes |
The cube |
3D pentominoes |
Maximizing |
|
POLYSEXES |
|
Sexominoes |
Xominoes |
Zucca's Puzzle |
Domino Puzzle |
SexCubes |
Dodecaculeus |
Tubominoes |
|
SEXEHEXES |
|
SexeHexeS For Sale |
More about SexeHexeS |
How we did it |
Other Sexehex Puzzle |
My Solution |
Reproduction |
|
POLYMULTIFORMS |
|
May-June edition |
PolyEdges |
To cover a solid |
Fourier Series of a Square |
Order 13 Perfect Square |
Fibonacci Machine |




 Index
Index




