Vorrei parlarvi di una piastrella, questa piccola piastrella qua sopra! La vidi per la prima volta in Tunisia, in una casa di Jerba, la famosa isola dei Lotofagi di cui parla Ulisse.

Ricordo ancora un angolino di una stanza d'ingresso, era fatto come la figura qua accanto. Guardandolo, ci misi un pò a capire che era composto da una piastrella sola. Pensavo, come si usa da noi, che fosse costituito da un coordinato. Voi direte: checc'entrano le piastrelle con un sito dedicato ai pentamini e ad altri puzzle? Beh, possiamo sempre considerare la piastrella come un... monomino!

Mi accorsi poi, girovagando per l'isola, che c'erano delle antiche fornaci dove costruivano varie forme di vasellame e una sola piastrella: questa.

E mi domandai per quale ragione il nostro mondo industrializzato non si fosse impossessato di questa forma che invece sembra proprio adatta alla costruzione in grande serie.

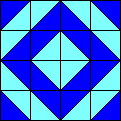
Si potrebbero, infatti, produrre piastrelle industrialmente in grande quantità, lasciando libera la fantasia dell'artigiano che le installa. Ecco ancora qualche esempio:

La seguente è comunque quella che preferisco. Si può proseguire costruendo all'infinito la spirale, oppure si possono affiancare gruppi come questo dopo averne applicato specularità orizzontali o verticali.

La piastrella tunisina ci ha fatto venire l'idea, forse non del tutto originale, di disegnarne una dove ciascun lato potesse combaciare con ciascun altro, senza essere uguale. Il risultato è stato gradevole. Con questa piastrella si possono comporre pavimenti geometrici di ripetizioni e simmetrie...

...oppure completamente casuali. In quest'ultimo caso, se ci provate, vedrete com'è divertente. Una piastrella tira l'altra, come le cigliegine. Noterete anche come il cordone che si forma passi, ad ogni incrocio, una volta sopra, una volta sotto. E ciò per qualunque combinazione adottiate. Urge una dimostrazione matematica!

Il risultato è ancor più caotico. Ma la regola del cordone che una volta passa sotto e una volta passa sopra sembra non più valere.