Se vuoi aver successo, parla di sesso. [mio nonno].

I think 'sexehexes' would be a better name for them.
Yes, that would be a perfect name! [Ed Pegg Jr]

Grazie, Ed, per questo sonoro palindromo.
Io, in italiano, non sono riuscito a fare altrettanto.

Dunque, se ripeto il ragionamento con gli esagoni, così come ho gia fatto con i quadrati e i triangoli, poi ho esaurito l'argomento. Infatti soltanto i triangoli, i quadrati e gli esagoni, tra i poligoni regolari, coprono il piano. Certo si potrebbero sessuare i tetramini, i pentamini, ma questo è un altro film.

Incominciamo a vedere quali e quanti sono tutti i possibili esagameti (one side): ecco 1 neutro, 2 etero e gli 11 bi-sex possibili:

Ventotto esagameti trisessuati:

Ben 42 tetrasessuati:

32 sono i pentasessuati (accettando i pezzi speculari, le combinazioni sono 2 elevato 5):

e infine 14 completi (notate come il numero 14 entra insistentemente):

Se escludete i pezzi speculari, quelli con l'asterisco, ottenete la serie rovesciabile. In totale sono 130 esagameti per la serie ad una faccia sola e 92 pezzi rovesciabili. Ad esempio possiamo disporre la prima serie in un pseudo-rettangolo di 14+15+14+15+14+15+14+15+14=130 esagoni (di nuovo il numero 14!). Questa è la migliore soluzione oggi nota, che ci perviene da Richard Dickson. Ottimo lavoro, Richard, anche se resto convinto che ne esistano con i bordi neutri, fino a che qualcuno non mi dimostri il contrario.

130 vale anche 12 al quadrato meno 14 (il numero 14 un'altra volta!). Ciò origina il rombo qua sotto di 12x12 esagoni con un buco di 14. E' carino, ma credo che sia impossibile (con l'orlo neutro).

Il prossimo, invece, è un interessante esagono di esagoni. E' costituito da 127 celle, ottenibili dalle nostre 130 scartandone tre.
DOMANDA: Esiste almeno una soluzione con il bordo diritto, cioè senza maschi o femmine?
RISPOSTA 1: Credo che non esista, anche se non ne ho la prova matematica.
RISPOSTA 2: Forse esiste, ma è quasi impossibile trovarla tra 10^300 combinazioni.
RISPOSTA 3: Eccola qua:

Appena posso, vi spiego come ci siamo arrivati. Si può fare lasciando fuori il Neutro, il Maschio e la Femmina? Se volete inviarmi una soluzione, la pubblicherò volentieri.

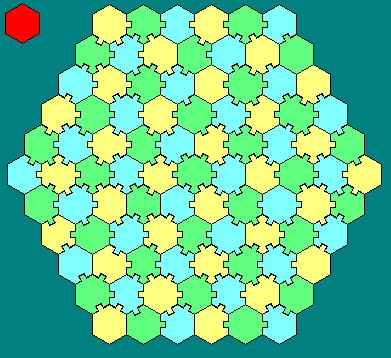
Ed Pegg Jr mi ha mandato la prima soluzione (ne avreste dubitato?). Lui dice (traduco): I 92 possibili esagameti rivoltabili mi sembrano ancora più interessanti dei 130 a una sola faccia. 91 pezzi possono formare un esagono. Chissà quanti lati esterni possono essere neutri, se lasciamo fuori il pezzo esattamente esagonale?

Io ho dipinto la mappa di Ed in funzione del numero di sessi di ciascun pezzo. Notate come la disposizione non sia affatto casuale.

Ma quanti lati esterni possono essere neutri?

I casi sono due: O esiste la soluzione completa, O la seguente è la migliore (e tassella l'infinito!).

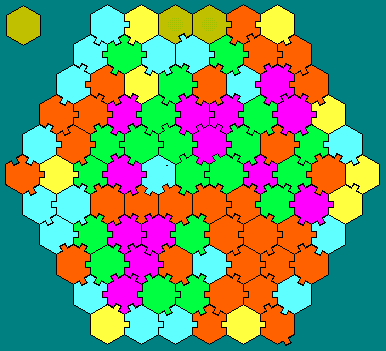
L'ultima figura è graziosa, ma non è la soluzione proposta da Ed. E' fatta da 91 pezzi prelevati dalla serie one-side di 130. La mia Darwin Machine ha impiegato 11 secondi per trovarla, e può scovarne molte altre. Però, se date esattamente questo sottoinsieme di pezzi ad un amico, scommetto che non lo risolverà.

Prima edizione: 20 feb 2000 - Ultima modifica: 12 mag 2000