PolyEdges
(Isoperimetric polygons)
When I was child the square was the polygon with four equal edges.
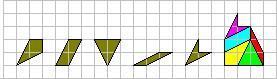
I define a series of polygons by their edges, on a squared grid. For example below there are the 5 possible polygons with perimeter = 2+2SQR(5).
Here there are the possible polyedges with perimeter = 3+3sqr(5). We could name them:
IsoPeriploes(3+3SQR5)
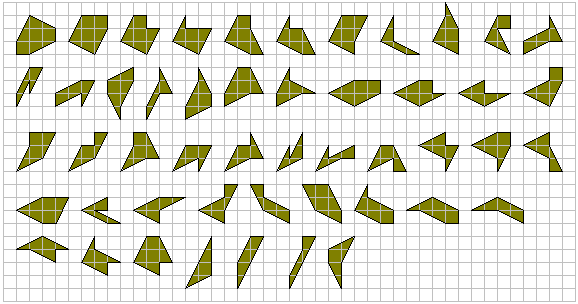
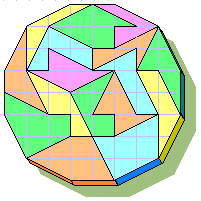
The IsoPeriploes(3+3SQR5) are triangles, quadrilaterals, pentagons or hexagons. Their area is always integer of 2, 3, 4, 5 or 6. It is possible to define many other PolyEdges.
The pieces have a good capability of aggregation (but it isn't trivial!):
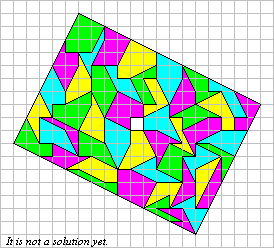
Not all IsoPeriploes(3+3SQR5) tile the plane, but someone do it with fantasy:
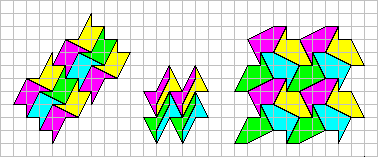
IsoPeriploes(n)
Isoperimetric Polyominoes

IsoPeriploes(10)

IsoPeriploes(12)
Order 12 Isoperimetric Polyominoes
It's better to define the pieces below as Order 12 Isoperimetric Polyominoes because as IsoPeriploes(12) there are pieces on squared grid which remember us the Pitagora's theorem.
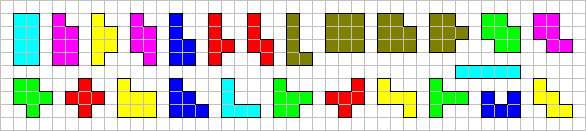
With these 25 pieces you could compose a 10x15 rectangle. You could see other constructions on the Andrew Clarke Polyominoes pages.

You must add these 9 pieces to obtain the complete series of IsoPeriploes(12) on squared grid. It's also possible to compose a trapezium with all the 34 pieces.
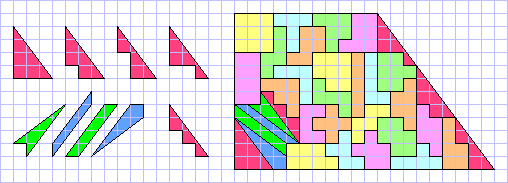
IsoPeriploes(2(2+SQR8+SQR10))
WARNING: the page is experimental, the sets could be incomplete, the puzzles not solvable.
_________________
First edition: 16 June 2000 - Last revision: 21 June 2000

| HOME | Pentominoes | More about pentominoes | The cube | 3D pentominoes | Polysexes | Sexominoes | Xominoes | SexeHexeS | SexeHexeS For Sale | More about SexeHexeS | How we did it | Other Sexehex Puzzle | Chronicle | My Solution | Zucca's Puzzle | Domino Puzzle | SexCubes | Dodecaculeus | Tubominoes | PolyMultiForms | Tiling | PolyEdges | Fourier Series of a Square | Order 13 Perfect Square | Fibonacci Machine | Download | Links |
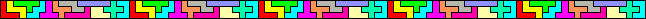


 Index
Index




