Contiamo le soluzioni dei Sexomini

Quante soluzioni ha il puzzle di 6x4 Sexomini non rovesciabili?
147.928
rotazioni e riflessioni escluse
Pierpaolo Bernardi - 2 Luglio 2001
Non mi sembravano tante la prima volta.
Il problema e' probabilmente risolvibile in vari modi, nessuno dei quali facilmente.
Se pensate di eseguire tutte le 24! permutazioni ruotando ogni sexomino
nelle posizioni possibili, otterrete 3x10^36 combinazioni. Se avete un
super PC che le esamini al ritmo di 1/nanosec, impiegherete 10^17 secoli.
Qualcuno ci sta provando, potando molti molti rami secchi. Se volete
provare a fare un programma ad hoc, tenete conto che:
1) soltanto 7 pezzi possono occupare gli angoli;
2) i pezzi full-sexed possono occupare solo i posti centrali;
3) i pezzi tri-sex non possono entrare nei posti centrali.
Giugno 2001 - Pierpaolo Bernardi sta tentando di risolvere il problema globale con un programma scritto in Common Lisp. Pare che sia vicino ad ottenere una soluzione al secondo. Se la mia stima di 250.000 probabili soluzioni e' attendibile, dovrebbe trovarle tutte in meno di tre giorni di calcoli continui!
2 Luglio 2001 - Pierpaolo ha concluso i suoi calcoli. Ecco le sue conclusioni:
...il numero di soluzioni, senza riflessioni è di 147.928, quindi
295.586 soluzioni totali. [Poiche' i pezzi sono per definizione non-rovesciabili, ogni riflessione e' in realta' un'altra soluzione. Noi, in seguito, per brevita' considereremo solo le soluzioni escluse le rotazioni e le riflessioni.]
Sono bastate circa 12 ore di calcolo.
Classificandole in base alla posizione del pezzo neutro si
possono ripartire come segue:
71.992 hanno il pezzo neutro in (1,1)
8.688 in (1,2)
5.928 in (3,1)
61.320 in (2,1)
In questo file potete trovare il programma in Common Lisp di Pierpaolo.
Qualcuno vuol confermare questi dati?
6 Agosto 2001 - Tocca al sottoscritto la verifica:
Con il solito Gerard's Polyomino Solution Engine, bloccando il pezzo neutro in posizione (1,2) e poi in posizione (3,1) verifico facilmente i blocchi di 8.688 e 5.928 soluzioni.Con il neutro in (2,1) riesco anche a confermare le 61.320 soluzioni, grazie ad alcuni artifici, ad un Pentium con clock di 1 GHz e ad un weekend di tempo macchina.
Ma l'analogo tentativo con il neutro in (1,1) provoca inevitabilmente l'inchiodamento della macchina dopo due giorni e una notte di lavoro. (Credo di aver individuato l'inconveniente in una protezione eccessiva di Microsoft in Internet Explorer: quando le soluzioni superano un certo numero, il sistema fa ricorso alla memoria virtuale, ma poiche' Java non deve scrivere sul disco, scatta la protezione).
La soluzione arriva con le... ferie:
L'importanza dell'ermafrodita
Sostituiti i lati sessuati con lati ermafrodita, cerco le soluzioni con neutro(1,1). Esse sono solo 10 (40 per il pezzo neutro in posizione qualunque):
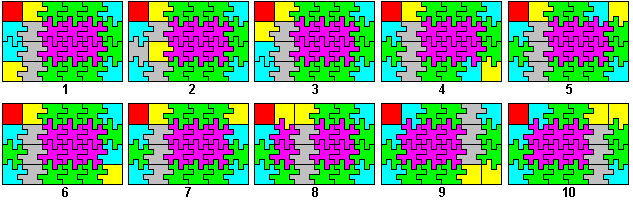
Queste vengono utilizzate come matrici dove i pezzi omologhi sono permutati solo tra loro, ottenendo un'accelerazione iperbolica. Sotto potete vedere come l'utilizzo di chiavi possa forzare un solver a permutare i pezzi solo dove servono:

Matrice 1
| Matrice | Nr. Sol. |
| 1 | 9312 |
| 2 | 7424 |
| 3 | 8688 |
| 4 | 6500 |
| 5 | 6044 |
| 6 | 7120 |
| 7 | 6796 |
| 8 | 6244 |
| 9 | 6760 |
| 10 | 7104 |
| Totale: | 71992 |
Le 71.992 soluzioni con il pezzo neutro in (1,1) sono quindi confermate. Il tempo macchina e' stato inferiore alla mezz'ora in tutto, con il solito solver in Java, chissa' cosa potrebbe diventare con un prg. ad hoc. Il metodo e' generalizzabile per tutte le altre sex-forms, anche per quelle che aspettano soluzioni... :o)
La transessualita' dei Sexomini
Un'ultima osservazione di Pierpaolo: invertendo contemporaneamente tutti i sessi ad una soluzione, se ne ottiene un'altra che non e' una rotazione o una riflessione della precedente. Si dovrebbe quindi poter dimezzare ulteriormente il tempo di ricerca:
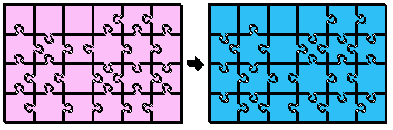
Cambiamento di sesso
L'osservazione di Pierpaolo ha numerose implicazioni. In primis, e' da molto tempo che mi chiedo (e chiedo ai NG :) una spiegazione del fatto che il numero delle soluzioni di tutti i sottoinsiemi osservati finora sia pari: la nota di Pierpaolo e' la risposta.
Mi e' poi capitato questo busillis: nel cercare le 61.320 soluzioni col neutro in (2,1) ho notato che in (1,1) poteva starci solo uno dei due monosessuati. Ho spezzato quindi il problema in due, imponendo in (1,1) prima la femmina e poi il maschio. Ho ottenuto due gruppi di 30.660 soluzioni cadauno e mi sono stupito di tanta simmetria: ora so il perche'!
Notiamo infine che questa transessualita' e' applicabile a tutte le Polysexes e in particolare ai SexeHexeS di cui possiamo ottenere altre soluzioni partendo dalle pochissime note.
Strategia ottimale
[IMHO] Ad oggi la strategia migliore per calcolare il numero delle soluzioni credo che sia la seguente: precalcolate le 40 matrici di ermafrodita, usarle per trovare 40 gruppi di soluzioni dove si potranno scambiare i pezzi soltanto tra quelli omologhi: 4 angolari, 3 bisex, 8 trisex e 6 full-sexed. L'ideale e' usare un buon linguaggio di programmazione compilabile. I due monosex potranno essere fissati in modo arbitrario: il numero delle soluzioni potra' essere moltiplicato per due, grazie alla simmetria transessuale. Se tanto mi da tanto, scommetto che si puo' abbattere il tempo di elaborazione a qualche minuto!
_________________
Classificazione di Dario Uri
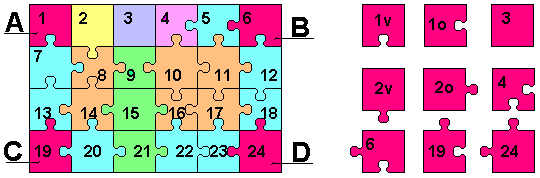
Alla luce della soluzione di Pierpaolo, questa strada puo' apparire laboriosa. Resta cmq. una strada percorribile che richiederebbe solo qualche volontario per essere completata. Dario Uri propose sul NG it.hobby.enigmi di spezzare il problema in 510 sottocasi, bloccando di volta in volta i pezzi d'angolo. Nacque la tabella qua sotto. Chissa' se un giorno riusciremo a vederla completata?
| Indice | A | B | C | D | N.Sol. | Autore | N.Sol. | Autore | N.Sol. | Autore |
| 1 | 1o | 2o | 3 | 4 | 0 | LZ | - | - | - | - |
| 2 | 1o | 2o | 4 | 3 | 0 | LZ | - | - | - | - |
| 3 | 1o | 3 | 2o | 4 | 0 | LZ | - | - | - | - |
| ... | ... | ... | ... | ... | ... | ... | - | - | - | - |
| 127 | 1v | 2o | 4 | 19 | 566 | Dario Uri | - | - | - | - |
| 128 | 1v | 2o | 19 | 4 | 258 | Dario Uri | - | - | - | - |
| 129 | 1v | 4 | 2o | 19 | 0 | Dario Uri | - | - | - | - |
| 130 | 1v | 4 | 19 | 2o | 410 | Dario Uri | - | - | - | - |
| 131 | 1v | 19 | 2o | 4 | 0 | Dario Uri | - | - | - | - |
| 132 | 1v | 19 | 4 | 2o | 414 | Dario Uri | - | - | - | - |
| 133 | 1o | 2v | 4 | 19 | 184 | LZ | 184 | Dario Uri | - | - |
| 134 | 1o | 2v | 19 | 4 | 460 | LZ | 460 | Dario Uri | - | - |
| 135 | 1o | 4 | 2v | 19 | 256 | Dario Uri | - | - | - | - |
| 136 | 1o | 4 | 19 | 2v | 310 | Dario Uri | - | - | - | - |
| 137 | 1o | 19 | 2v | 4 | 184 | Dario Uri | - | - | - | - |
| 138 | 1o | 19 | 4 | 2v | 506 | Dario Uri | - | - | - | - |
| 139 | 1v | 2v | 4 | 19 | 378 | Dario Uri | - | - | - | - |
| 140 | 1v | 2v | 19 | 4 | 744 | Dario Uri | - | - | - | - |
| 141 | 1v | 4 | 2v | 19 | 0 | LZ | 0 | Dario Uri | - | - |
| 142 | 1v | 4 | 19 | 2v | 936 | Dario Uri | - | - | - | - |
| 143 | 1v | 19 | 2v | 4 | 0 | LZ | 0 | Dario Uri | - | - |
| 144 | 1v | 19 | 4 | 2v | 1288 | Dario Uri | - | - | - | - |
| ... | ... | ... | ... | ... | ... | ... | - | - | - | - |
| 175 | 1v | 2o | 6 | 19 | 324 | Dario Uri | - | - | - | - |
| 176 | 1v | 2o | 19 | 6 | 390 | Dario Uri | - | - | - | - |
| 177 | 1v | 6 | 2o | 19 | 232 | Dario Uri | - | - | - | - |
| 178 | 1v | 6 | 19 | 2o | 176 | Dario Uri | - | - | - | - |
| 179 | 1v | 19 | 2o | 6 | 236 | Dario Uri | - | - | - | - |
| 180 | 1v | 19 | 6 | 2o | 268 | Dario Uri | - | - | - | - |
| 181 | 1o | 2v | 6 | 19 | 390 | Dario Uri | - | - | - | - |
| 182 | 1o | 2v | 19 | 6 | 324 | Dario Uri | - | - | - | - |
| 183 | 1o | 6 | 2v | 19 | 236 | Dario Uri | - | - | - | - |
| 184 | 1o | 6 | 19 | 2v | 176 | Dario Uri | - | - | - | - |
| 185 | 1o | 19 | 2v | 6 | 232 | Dario Uri | - | - | - | - |
| 186 | 1o | 19 | 6 | 2v | 268 | Dario Uri | - | - | - | - |
| 187 | 1v | 2v | 6 | 19 | 498 | Dario Uri | - | - | - | - |
| 188 | 1v | 2v | 19 | 6 | 498 | Dario Uri | - | - | - | - |
| 189 | 1v | 6 | 2v | 19 | 0 | LZ | 0 | Dario Uri | - | - |
| 190 | 1v | 6 | 19 | 2v | 748 | Dario Uri | - | - | - | - |
| 191 | 1v | 19 | 2v | 6 | 0 | LZ | 0 | Dario Uri | - | - |
| 192 | 1v | 19 | 6 | 2v | 700 | Dario Uri | - | - | - | - |
| ... | ... | ... | ... | ... | ... | ... | - | - | - | - |
| 507 | 4 | 19 | 6 | 24 | 0 | LZ | - | - | - | - |
| 508 | 4 | 19 | 24 | 6 | 0 | LZ | - | - | - | - |
| 509 | 4 | 24 | 6 | 19 | 0 | LZ | - | - | - | - |
| 510 | 4 | 24 | 19 | 6 | 0 | LZ | - | - | - | - |
Saro' felice di ricevere soluzioni parziali, totali, stime statistiche, osservazioni, verifiche, etc....
Chi non sapesse da che parte cominciare, puo' fare il download di un
mio programmino che aiuta:
http://members.theglobe.com/liviozucca/download/gerard1.zip
E' gratis (freeware) [1.5MB, ci vogliono 5..10 min di pazienza].
Lo potete unzippare con Winzip o equivalente e poi lanciate Setup.exe
per installarlo. E' la versione 1.0 con un failetto di help in italiano.
Dario Uri ha anche trovato il numero di soluzioni, escludendo rotazioni e riflessioni, di ciasun sotto-rettangolo:
| Indice | Rettangolo | N.soluzioni |
| 1 | 2x2 | 3 |
| 2 | 2x3 | 72 |
| 3 | 2x4 | 562 |
| 4 | 3x3 | 1.337 |
| 5 | 2x5 | 3.610 |
| 6 | 3x4 | 79.126 |
| 7 | 2x6 | 15.302 |
| 8 | 3x5 | 821.274 |
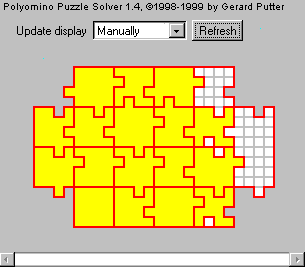
Qua sotto il solver di Gerard Putter tenta di trovare le soluzioni approssimando i sexomini con normali polimini:
_________________
First edition: Jun 28th, 2001 - Last revision: Aug 13th, 2001

|
HOME |
|
e-mail |
Download |
Links |
Chronicle |
|
PENTOMINOES |
|
More about pentominoes |
The cube |
3D pentominoes |
Maximizing |
|
POLYSEXES |
|
Sexominoes |
Xominoes |
Zucca's Puzzle |
Domino Puzzle |
SexCubes |
Dodecaculeus |
Tubominoes |
|
SEXEHEXES |
|
SexeHexeS For Sale |
More about SexeHexeS |
How we did it |
Other Sexehex Puzzle |
My Solution |
Reproduction |
|
POLYMULTIFORMS |
|
Aug 2000 edition |
May 2000 edition |
PolyEdges |
To cover a solid |
Fourier Series of a Square |
Order 13 Perfect Square |
Fibonacci Machine |



 Index
Index




