Polysexes

This page is an attempt to generalize the concept which inspired the Sexominoes, the SexeHexeS, the Xominoes and the Zucca's Puzzle.

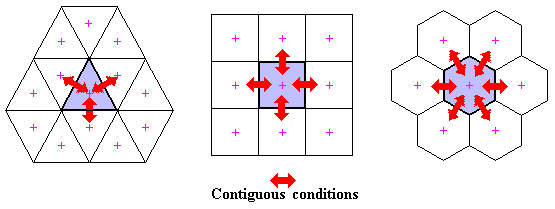
Among the regular polygons, the triangles, the squares and the hexagons tile the plain. I introduced conditions between contiguous edges. The condition could be: sex as the SexeHexeS and the Sexominoes, a more complex function as the Xominoes, drafters as Zucca's Puzzle. But also it could be different colors, mechanical keys, magnetic fields, electronic valences, human likes and dislikes...

Each piece has a barycenter, sometime not a true barycenter, but a point of rotation which can be placed on a grid: a hexagonal grid if the pieces are triangles, a square grid if the pieces are squares, a triangular grid if the pieces are hexagonal.

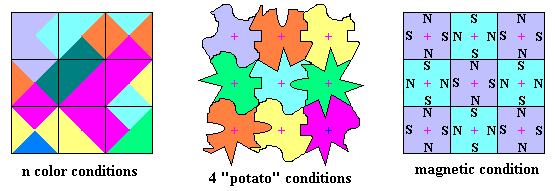
The possible pieces are a sub-set of:

N = (number of edge-forms)^(number of edges)
This number includes the rotations which you must eliminate, if you want 1-side different pieces only. You must eliminate the mirror pieces yet, if you want 2-side different pieces only.

The condition could be:

SIMPLE & FLIPPABLE as Sexominoes, SexeHexeS, Color-condition.

SIMPLE & NOT FLIPPABLE as Potato-condition, if the edges have not symmetry.

COMPLEX as Xominoes and Zucca's Puzzle, where the conditions could involve more edges or where the condition could change flipping the piece.

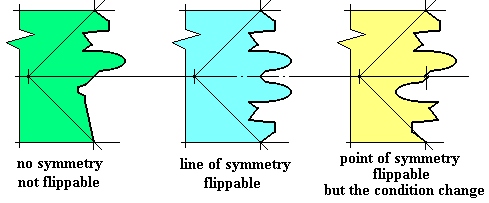
If the conditions are simple, we could attempt a classification. Below there are the numbers of different pieces:

Nr. edge-forms	TRIANGLE 1-SIDE	TRIANGLE 2-SIDE	SQUARE 1-SIDE	SQUARE 2-SIDE	HEXAGON 1-SIDE	HEXAGON 2-SIDE
1	1	1	1	1	1	1
2	4	4	6	6	14	13
3	11	10	24*	21	130**	92**
4	24	20	70	55	700	430
5	45	35	165***	120	...	...
6	76	56	336	231	...	...
7	119	84	616	406	...	...
8	176	120	1044	666****	...	...

* Sexominoes - ** SexeHexeS - *** 1-side Xominoes - **** Biblical!

___________

New examples

Biblical or Fourier's Puzzle

666 pieces = 37x18 rectangle with sinusoidal edge (odd armonics).
Do you remember the Fourier Series?
sin(x)+sin(3x)/3+sin(5x)/5+sin(7x)/7+...
generates a square wave!

___________

Faces Puzzle

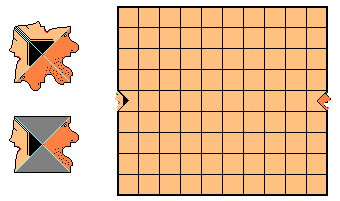
90 2-side pieces = 10x9 rectangle. This simple puzzle has "complex" conditions.

___________

Email

If you have an interest in the mathematical aspect of the puzzles, read this interesting email from Chris Hartman.

If you like, send me an email here.

___________

A note

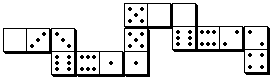
Many centuries ago, perhaps in Mesopotamia, the ancient Arabs invented a two squares based game, with seven contiguous conditions: it is the Domino.
Oh! It's an idea!

___________

I think that many molecules and many crystals are similar puzzles. It's naturally possible to apply the concept to 3-dimension or n-dimension space, but this will be an other page.

1st edition: 14 Apr 2000
| POLYSEXES | Sexominoes | Xominoes | SexeHexeS | More about SexeHexeS | How we did it | Other Sexehex Puzzle | Chronicle | My Solution | Zucca's Puzzle | Domino Puzzle |

| Pentominoes | More about pentominoes | The cube | 3D pentominoes | Fibonacci Machine | Download | Links |