Maximum Polygons
Livio Zucca
We define "Order N Maximum Polygon" the equilateral polygon with N unitary edges and greatest area that tiles the plane.
| Order | Polygon | Area | Tiling |
| 3 | 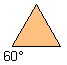 | 0.433013- |  |
| 4 | 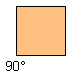 | 1 | 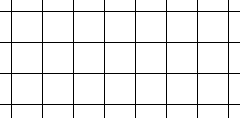 |
| 5 | 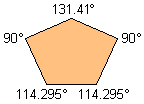 | 1.661438- | 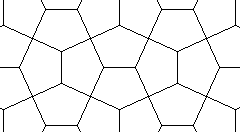 |
| 6 | 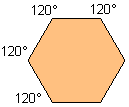 | 2,598076+ | 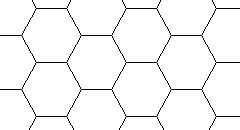 |
| 7 | 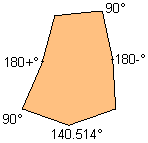 | 3.089725- | 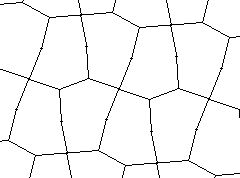 |
| 8 | 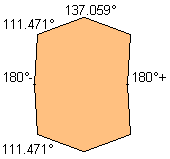 | 4.403+ | 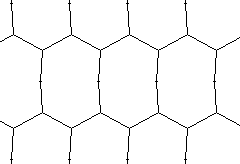 |
| 9 | 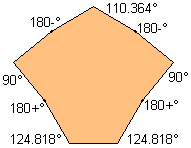 | 5.391941+ | 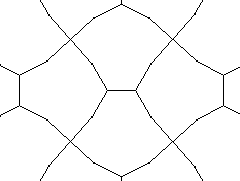 |
| 10 | 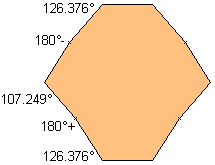 | 7.0406+ | 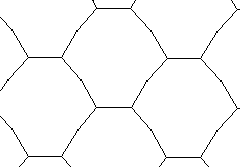 |
Generalization
All the Order N Maximum Polygon, for N>=6 and N even, are in the form below:
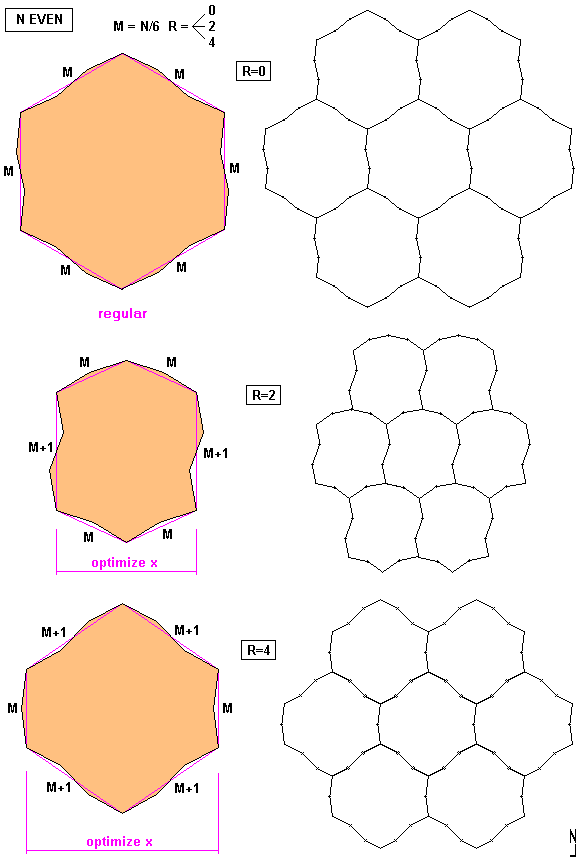
For N even and alpha -> 180°
For R=0:
Area = M^2*sqr(3)*3/2
For R=2:
Area = ...
For R=4:
Area = ...
All the Order N Maximum Polygon, for N>=5 and N odd, are in the form below:
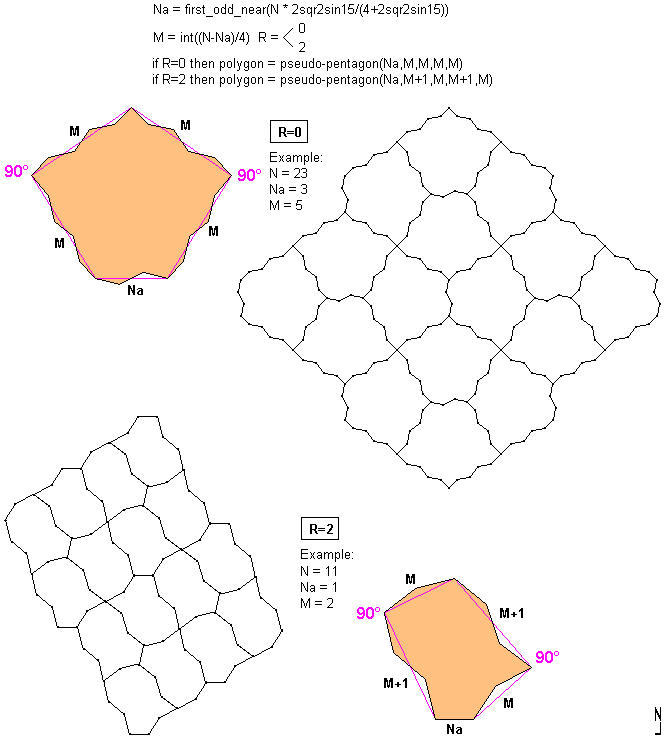
For N odd and alpha -> 180°
For R=0:
Area = Sqr(2*M^2-(Na/2)^2)*Na/2+M^2
For R=1:
Area = Sqr((M+1)^2+M^2-(Na/2)^2)Na/2+M*(M+1)
Notice: on this page there is only a my conjecture. Many data are unproved. You could find a bigger polygon than these that tiles the plane. But I think it is improbable.
_________________
It isn't trivial!
First edition: Oct 28th, 2003 - Last revision: Nov 6th, 2003




 Index
Index




