The Hypercube
I'll use the 4-dimensional axonometry below:
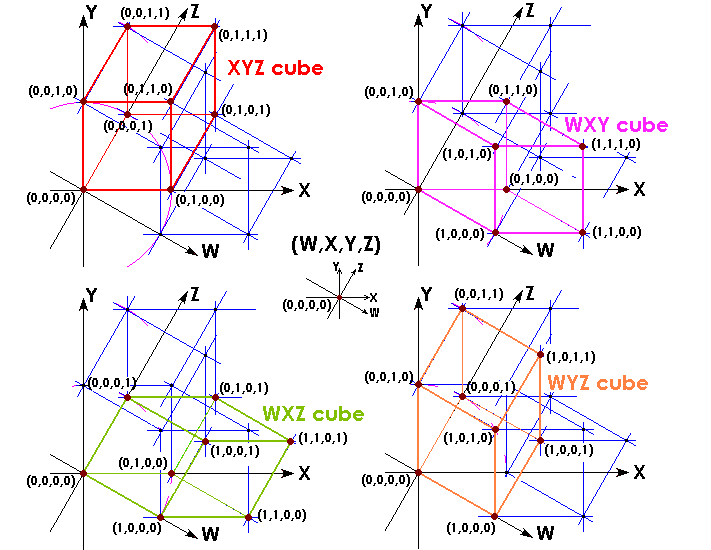
The a 4-dimensional axonometry has the same roules of the 3-dimensional axonometry:
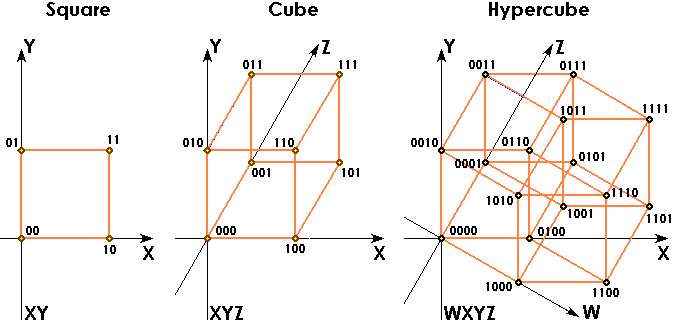
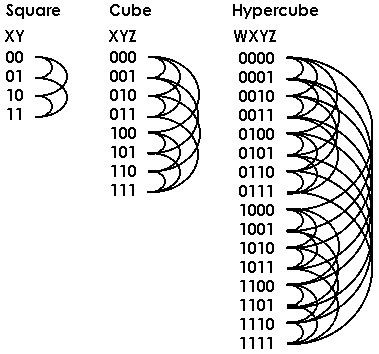
I like more this axonometry rather than the traditional graph because it has less overlaps when we build the polyhypercubes. Notice: each edge connects the coordinates that change one only bit. Therefore these are the graphos of a square, a cube and a hypercube:
Following the colors, we can see easily the 8 cubes. Each face belongs to 2 cubes, each edge belongs to 3 cubes and each vertex belongs to 4 cubes:
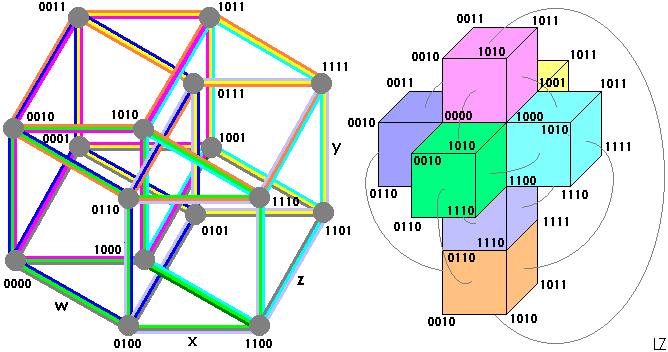
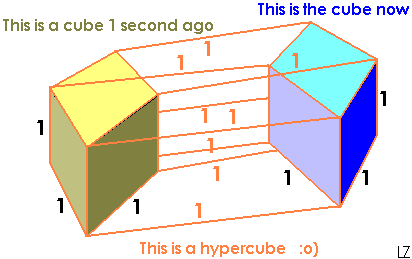
The 4D hypercube has 8 cells, 24 faces, 32 edges and 16 vertices. On the right you can see one of the possible 3D nets of the hypercube. The cubes have the same color that in the 4D axonometry, on the left.
Notice: Usually we name "hypercube" the generalization of a 3-cube to n dimensions and "tesseract" the 4D hypercube. In these pages I use generally the term hypercube for 4D hypercube.
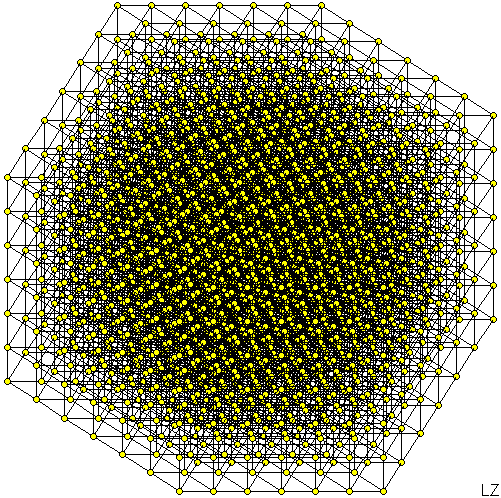
A 7x7x7x7 Hypercube axonometry.
Links:
mathworld.wolfram.com/Hypercube.html
en.wikipedia.org/wiki/Hypercube
_________________
It isn't trivial!
First edition: Mar 18th, 2006 - Last revision: Apr 10th, 2006

Copyrights 2006 Livio Zucca




 Index
Index




