It's the 24-cell, the hyperdiamond. I love this hyperpolyhedron. I think it's the VI Plato's Polyhedron because it has not a corresponding regular solid in 3D. It's self-dual: the barycentres of its 24 octahedra are the vertices of an other hyperdiamond. I don't like the graphos that you can find on-line, so I did re-draw it as below:

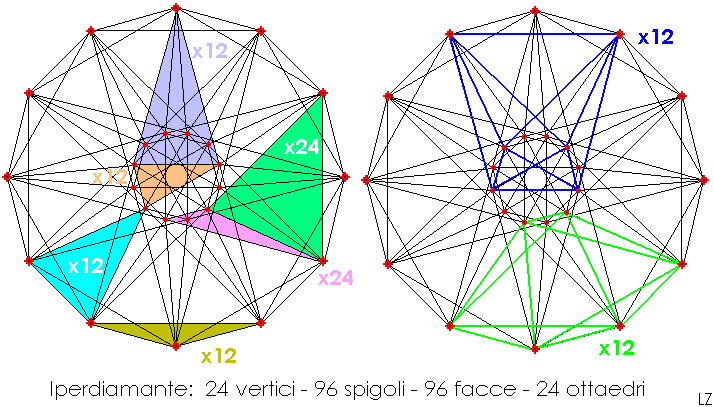
Now you can easily count the 24 vertices, the 96 edges, the 96 faces and the 24 octahedra.

Below there is a study of an axonometry:

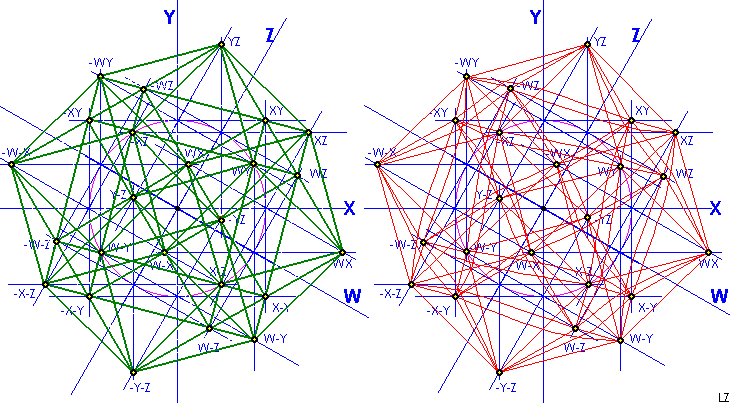
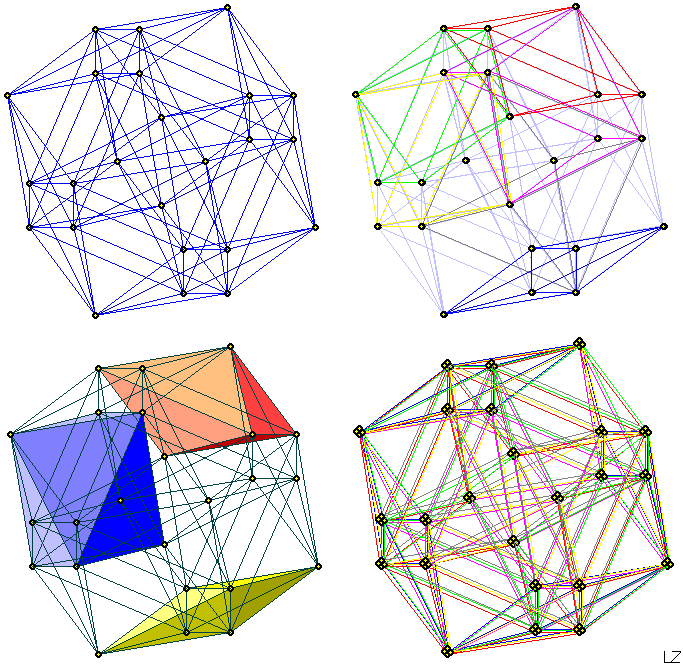
Links:
mathworld.wolfram.com/24-Cell.html

_________________

It isn't trivial!

First edition: Mar 18th, 2006 - Last revision: Mar 18th, 2006

Copyrights 2006 Livio Zucca