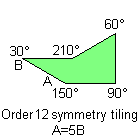
This pentagon has the property of the 1st family, two consecutive complementary to 180° angles, and the property of the 4th family, two non-consecutive complementary to 360° angles. The angle of 30° and the angle of 60° allow to tile the plane with order 6 and order 12 rotational symmetry. The A=5B property allows other interesting tilings.

You can see below the order 12 rotational symmetry tiling.

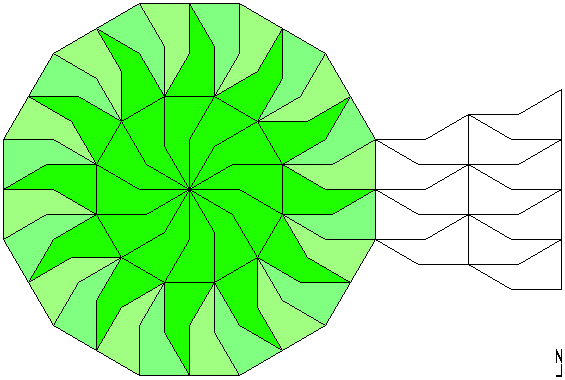
The tiling can continue to infinity.

And below there is the order 6 rotational symmetry tiling.

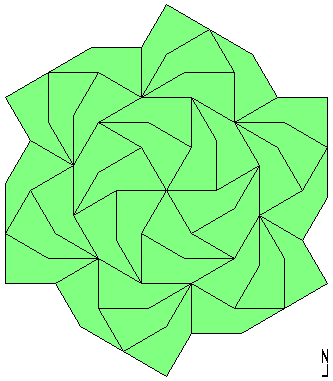
Next tiling is the most famous: 12 pentagons forms a regular dodecagon that tiles the plane with the help of other 4 pieces:

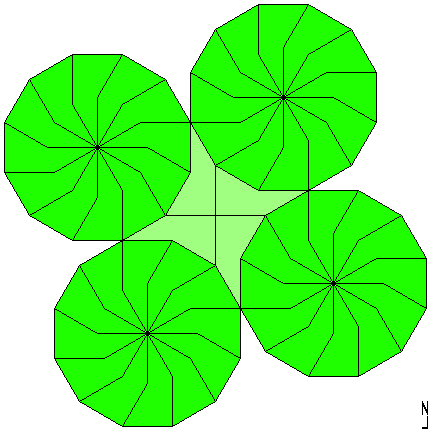
Now we use the A=5B property. The elegant symmetrical configuration of 10 pieces tiles the plane with the help of other two pentagons:

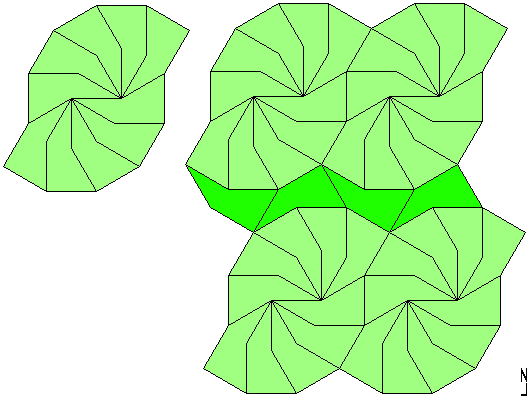
Below we demonstrate that this pentagon can tile 1/4 of the infinite plane.

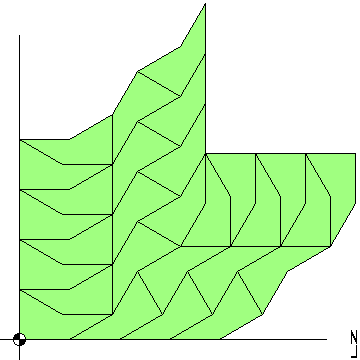
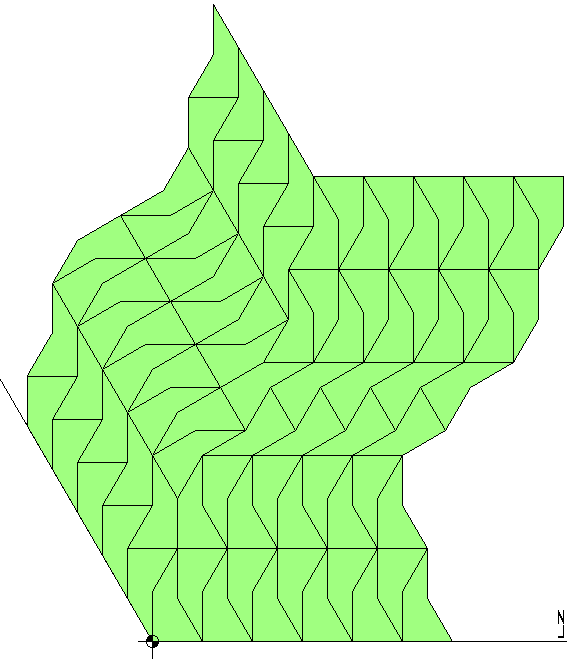
At last, a labouriosus demonstration that can tile 1/3 of the infinite plane: