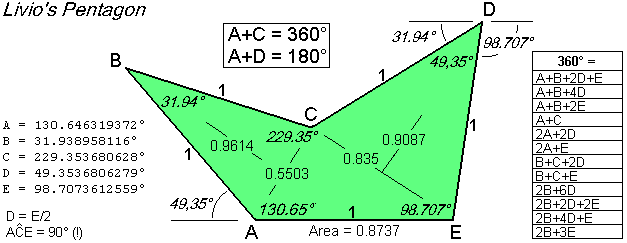
The story began the day that I checked the tiling of the convex (non-equilateral) pentagon that you see below. This tiling is not present on the list of the 14 convex pentagons that tile the plane because this pentagon is considered a subset of the Type 2, despite the topology is very different.

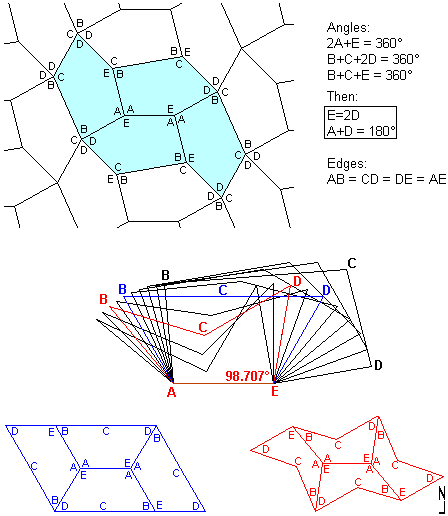
This convex pentagon has 4 equal edges. If you want to impose equal the 5th, you'll obtain the false-pentagon (blue), a trapezium. But if you continue the quest, you'll find a concave equilateral pentagon (red).

Obviously this new pentagon tiles the plane with the same topology of the non-equilateral first:

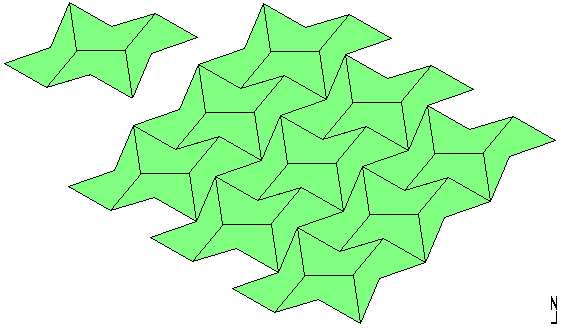
It allows also the Cairo tiling below and all the general tilings for the property: A+C = 360°.

For the property B+C+E = 360°, it's possible this hexagon with parallel edges:

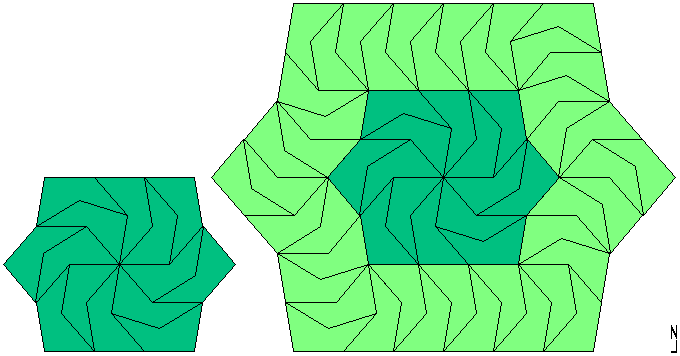
For the property 2B+2D+2E = 360°, this interesting decagon:

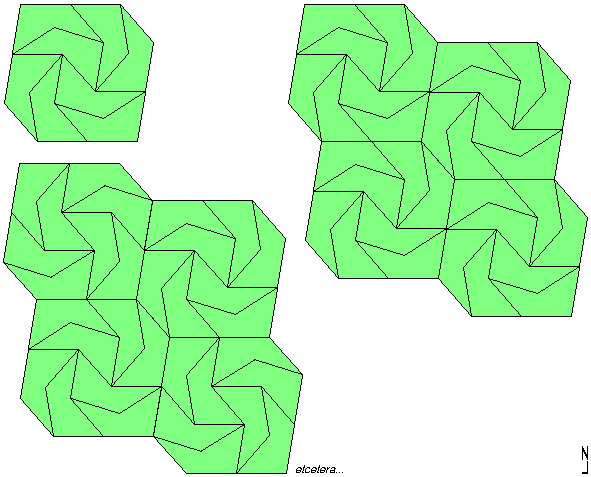
For the property 2B+6D = 360°, this decagon that we can multiply to infinity:

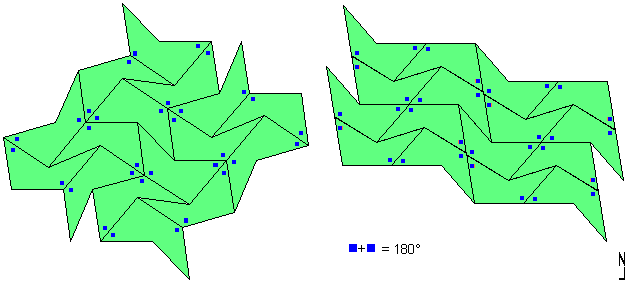
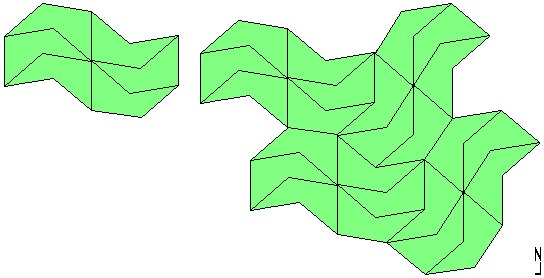
For all its properties, this chaotic tiling:

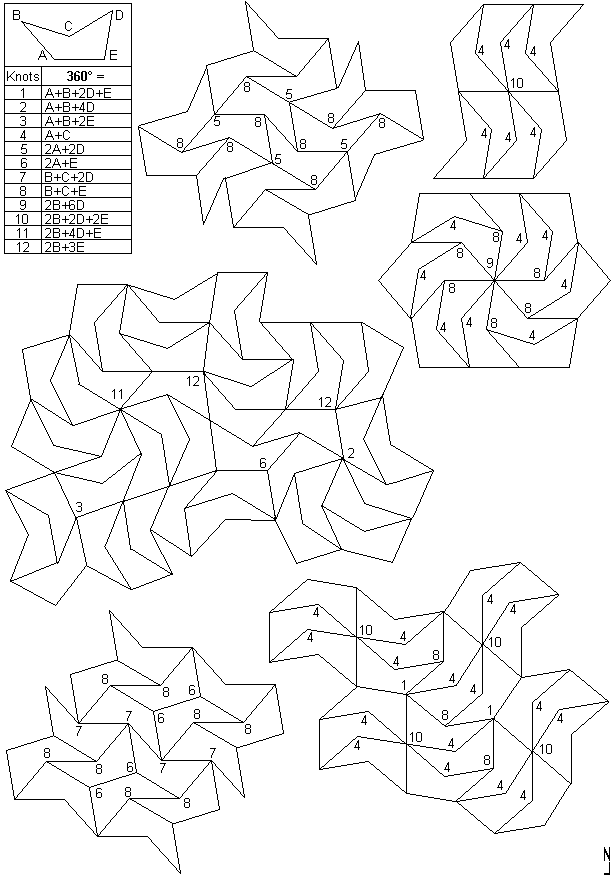
An example for each type of knot: