PolyHypercubes

The polyhypercubes are groupings of hypercubes joined by a cube. They are named also 4-dimensional polyominoes or polytesseracts. The number of the possible polyhypercubes is listed on sequence A068870 of The On-Line Encyclopedia of Integer Sequences. The author Frank Adams-Watters defines it as "Number of polyhypercubes or 4-dimensional polyominoes with n cells":

1, 1, 2, 7, 26, 147, 1019, 8699, 82535, ...

It is the number of polytesseracts where all symmetries are removed, in practice: 4D polycubes in multi-D space. An other interesting sequence is the A048665:

1, 8, 84, 936, 10810, 127632, 1531180, 18589840, ...

that is defined by the author Dan Hoey as "Number of rooted 4-dimensional "polycubes" with n cells, with no symmetries removed". The A005519:

1, 1, 2, 7, 26, 153, 1134, 11050, 128987, ...

contains the number of distinct d-dimensional polyominoes (or polycubes) with n cells, in practice: multi-D polycubes in multi-D space, as you can see on this pdf document by Rich Schroeppel. From this document I have extracted the table below by Dan Hoey & Bill Gosper:

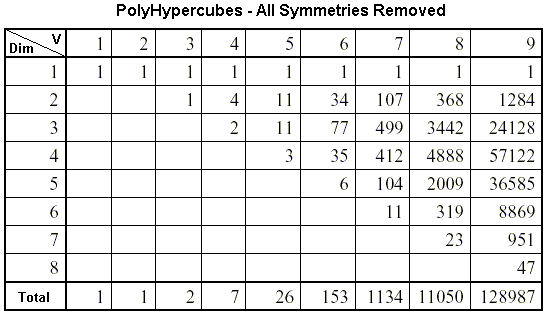
From all the on-line material I have also extracted this table:

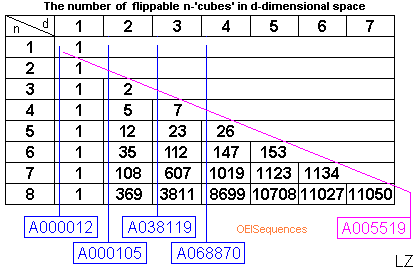
Last but not least, we take an interest in the sequence:

1, 1, 2, 7, 27, 164, 1316, ?, ...

that contains the number of 4D polycubes in 4D space. I have calculated the values 164 and 1316 with the bruteforce. The table below shows the analogy with the 2D and 3D non-flippable polyominoes:

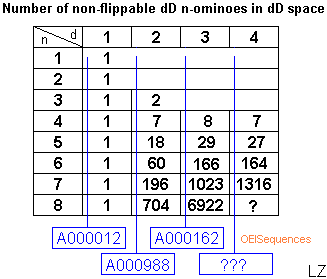
Tetrahypercubes

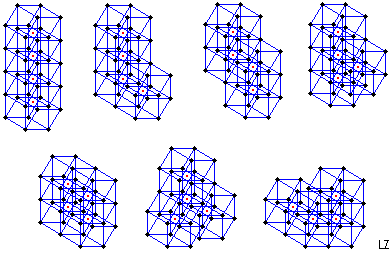
These are the seven tetrahypercubes. Remarke that they are only seven and not eight as the tetracubes. This because the 7.th coincides with its symmetric image in a 4D Euclidean space. I marked in red the barycentre of each hypercube.
Examine now the image below. It's a 2x2x2x2 hypercube. The barycentre of each 1x1x1x1 hypercube is marked in red. Obviously these 16 points are the vertices of a central hypercube (in red).

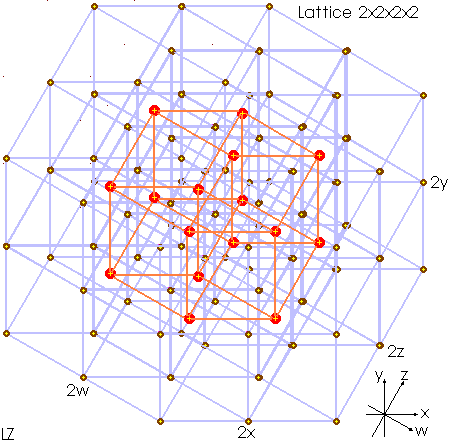
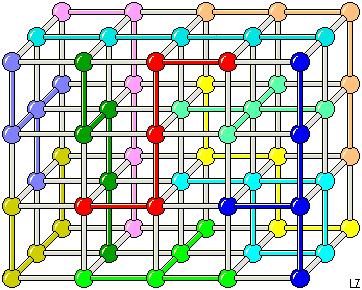
This fact help myself drawing a diagram of polycubes and polyhypecubes. For example, below we have the famous 12 solid pentominoes in a 3x4x5 3D space. The balls are the barycentres of each cube of the pentacubes. The segments are the faces of the cubes and they are colored if internal faces of the polycubes.

We can do the same thing with the polyhypercubes into a hyperlattice:

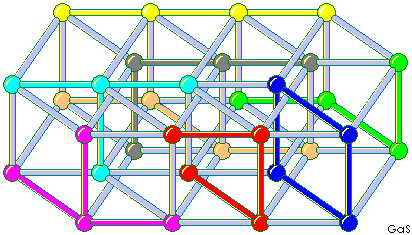
This is a 2x2x2x4 hyperspace filled with 7+1 tetrahypercubes (the 7.th is repeated). The solution is by Gabriele Carelli. Here also, the balls represent the barycentres of each hypercube and the colored segments represent the common cubes of each polyhypercube.

Pentahypercubes

The 4D pentahypercubes in 4D space are 27:

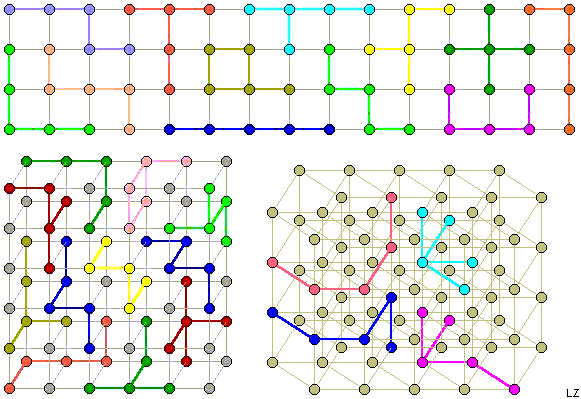
It's interesting to compose a 3x3x3x5 box:

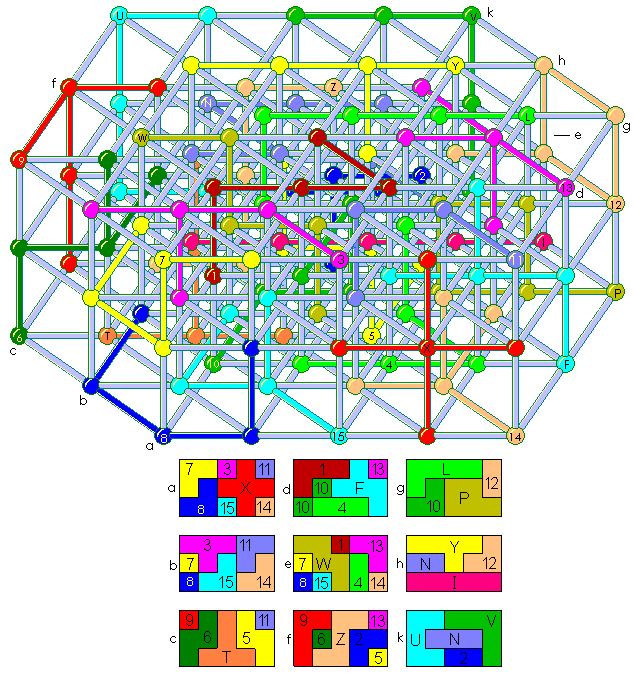
This is a 3x3x3x5 hyperbox, filled with the 27 pentahypercubes. The solution is copied from Andrew Clarke's site. Below the same axonometry, designed by a software that optimizes the minimal vertices overlap:

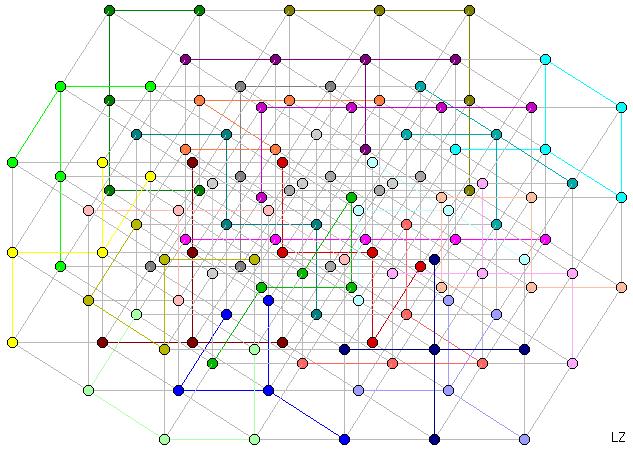
Ishino Keiichiro has found many other solutions to the 3x3x3x5 box. See his page.

_________________

It isn't trivial!

First edition: Mar 18th, 2006 - Last revision: Apr 6th, 2006

Copyrights 2006 Livio Zucca